
| ���������� | 50 | 100 | 200 | 500 | 1000 |
| �μӡ����������ɡ����� | 21 | 45 | 79 | 200 | 401 |
| �μӡ����������ɡ�Ƶ�� | 0.360 | 0.450 | 0.395 | 0.400 | 0.401 |
���� ��1�����ø��ʹ�ʽֱ�ӵó��𰸣�
��2�������ñ��������ݽ������Ƴ��μӡ����������ɡ������ĸ��ʣ�
�����â����������ó��μӡ����������ɡ���������
��� �⣺��1����С���μ��˸������µ�־Ը�߷���������ί�������־Ը�߷��䵽������Ŀ�飬
��С�������䵽�����������ɡ���Ŀ��ĸ���Ϊ��$\frac{1}{3}$��
�ʴ�Ϊ��$\frac{1}{3}$��
��2�����ɱ��������ݿɵã��������²μӡ����������ɡ������ĸ���Ϊ��0.4��
�ʴ�Ϊ��0.4��
�ڲμӡ����������ɡ��������ǣ�30000��0.4=12000���ˣ���
���� ������Ҫ����������Ƶ�ʹ��Ƹ��ʣ���ȷ����Ƶ�������֮��Ĺ�ϵ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
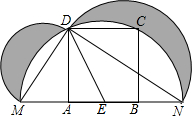 ��ͼ���ڱ߳�Ϊ6��������ABCD�У�E��AB���е㣬��EΪԲ�ģ�EDΪ�뾶����Բ����A��B���ڵ�ֱ����M��N���㣬�ֱ���ֱ��MD��NDΪֱ������Բ������Ӱ�������Ϊ��������
��ͼ���ڱ߳�Ϊ6��������ABCD�У�E��AB���е㣬��EΪԲ�ģ�EDΪ�뾶����Բ����A��B���ڵ�ֱ����M��N���㣬�ֱ���ֱ��MD��NDΪֱ������Բ������Ӱ�������Ϊ��������| A�� | 9$\sqrt{5}$ | B�� | 18$\sqrt{5}$ | C�� | 36$\sqrt{5}$ | D�� | 72$\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a��1�������»������ʽa+$\sqrt{{a}^{2}-2a+1}$�Ľ��Ϊ2a-1 | |
| B�� | ��a+$\sqrt{{a}^{2}-2a+1}$��ֵ��Ϊ��ֵʱ����ĸa��ȡֵ��Χ��a��1 | |
| C�� | a+$\sqrt{{a}^{2}-2a+1}$��ֵ��a�仯���仯����aȡij����ֵʱ����������ʽ��ֵ����Ϊ$\frac{1}{2}$ | |
| D�� | ��$\sqrt{{a}^{2}-2a+1}$=��$\sqrt{a-1}$��2������ĸa��������a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com