
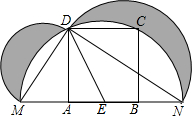
 如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )
如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为( )| A. | 9$\sqrt{5}$ | B. | 18$\sqrt{5}$ | C. | 36$\sqrt{5}$ | D. | 72$\sqrt{5}$ |
分析 根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积-大半圆的面积,MN的半圆的直径,从而可知∠MDN=90°,在Rt△MDN中,由勾股定理可知:MN2=MD2+DN2,从而可得到两个小半圆的面积=大半圆的面积,故此阴影部分的面积=△DMN的面积,在Rt△AED中,DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,所以MN=6$\sqrt{5}$,然后利用三角形的面积公式求解即可.
解答 解:根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积-大半圆的面积.
∵MN是半圆的直径,
∴∠MDN=90°.
在Rt△MDN中,MN2=MD2+DN2,
∴两个小半圆的面积=大半圆的面积.
∴阴影部分的面积=△DMN的面积.
在Rt△AED中,DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∴阴影部分的面积=△DMN的面积=$\frac{1}{2}MN•AD$=$\frac{1}{2}×6\sqrt{5}×6=18\sqrt{5}$.
故选:B.
点评 本题主要考查的是求不规则图形的面积,将不规则图形的面积转化为规则图形的面积是解答此类问题的常用方法,发现阴影部分的面积=△DMN的面积是解题的关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 旅客上飞机前的安检 | B. | 学校招聘教师,对招聘人员的面试 | ||
| C. | 了解一批灯泡的使用寿命 | D. | 了解701班的身高情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
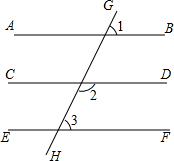 如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD
如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 调查总人数 | 50 | 100 | 200 | 500 | 1000 |
| 参加“迷你马拉松”人数 | 21 | 45 | 79 | 200 | 401 |
| 参加“迷你马拉松”频率 | 0.360 | 0.450 | 0.395 | 0.400 | 0.401 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com