
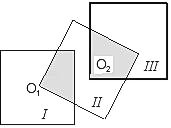
����Ŀ����ͼ�������ɸ��߳�Ϊ2�������Σ��������ε�һ����������������������O1����ͼ��ʾ�����Ƶ�����������һ����������������������O2���������������������������ص���������ɸ������ζ������ַ���ƴ�ӣ���Ҫm����������ʹƴ�Ӵ���ͼ�ε���Ӱ���ֵ��������һ�������ε����������һ������y=mx2+nx+3���䶥����x���ϣ���������ߵĶԳ���Ϊ_____��
���𰸡�x=��![]() ��
��
��������
���������ε����ʵó�S��NO1M=![]() S������1��������ȫ�����������ʵó�S�ı���NCO1E=S��NO1M��ͬ���ɵø���Ӱ����������ι�ϵ���������m��ֵ��Ȼ����ݶ������������0���n��ֵ���Ӷ�����������ĶԳ�����
S������1��������ȫ�����������ʵó�S�ı���NCO1E=S��NO1M��ͬ���ɵø���Ӱ����������ι�ϵ���������m��ֵ��Ȼ����ݶ������������0���n��ֵ���Ӷ�����������ĶԳ�����
��������������������
��O1�������εı�AN��MN�Ĵ���O1F��O1E������ֱ�ΪF��E������O1N��O1M��
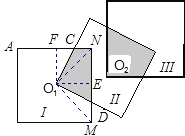
��O1Ϊ����������ģ�
��O1N=O1M����O1NC=��O1MD=45�㣬��NO1M=90�㣬
S��NO1M=![]() S������1��
S������1��
�ߡ�CO1N+��NO1D=��CO1D=90�㣬��DO1M+��NO1D=��NO1M=90�㣬
���CO1N=��DO1M��
����NCO1����MDO1��
�ߡ�O1NC=��O1MD��O1N=O1M����CO1N=��DO1M��
���NCO1�ա�MDO1��ASA����
��S��NCO1=S��MDO1��
��S�ı���NCO1D=S��NO1M��
�����������������غϲ��ֵ���Ӱ�������Ϊ�����������![]() ��
��
����Ҫ5��С��������ʹƴ�ӳ���ͼ�ε���Ӱ�����������һ��С�����ε������
��m=5��
��������y=5x2+nx+3�Ķ�����x���ϣ�
��![]() ��
��
��n=��2![]() ,
,
��y=5x2��2![]() x+3
x+3
��Գ���x=��![]() ��
��
�ʴ�Ϊ��x=��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
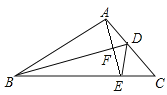
����Ŀ����ͼ������ABC�У���E��BC���ϵ�һ�㣬����AE��BD��ֱƽ��AE������ΪF����AC�ڵ�D������DE.
��1������ABC���ܳ�Ϊ18����DEC���ܳ�Ϊ6����AB�ij���
��2����![]() ,
,![]() ����
����![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
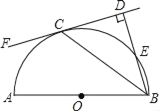
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����C�ǰ�ԲO�ϵ�һ�㣬CF�а�ԲO�ڵ�C��BD��CF��Ϊ��D��BD���ԲO���ڵ�E��
(1)��֤��BCƽ����ABD��
(2)��DC=8��BE=4����Բ��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
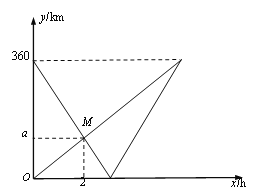
����Ŀ���쳵�������ֱ��A�к�B������ͬʱ������������ʻ����������У���������A�к�ֹͣ��ʻ���쳵����B�к�������ԭ·ԭ�ٶȷ���A�У���ͷʱ����Բ��ƣ������������ͬʱ����A�У��졢��������B�е�·��y1��y2����λ��km�������ʱ��x����λ��h��֮��ĺ���ͼ����ͼ��ʾ��
��1��A�к�B��֮���·���� km��
��2����a��ֵ��������ͼ�е�M�ĺ����ꡢ�������ʵ�����壻
��3���쳵������ӭ�������Ժ��پ����ʱ���������20 km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��BC�ཻ�ڵ�O��AC=BD����C =��D=90����
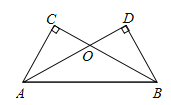
��1����֤��OA=OB��
��2������ABC=30����OC=5����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
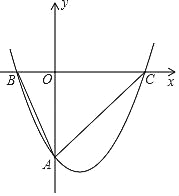
����Ŀ����ͼ��������A��0����4����������y=![]() x2+bx+c��x���ཻ�ڵ�B����2��0����C��OΪ����ԭ�㣮
x2+bx+c��x���ཻ�ڵ�B����2��0����C��OΪ����ԭ�㣮
��1���������߽���ʽ��
��2����������y=![]() x2+bx+c����ƽ��
x2+bx+c����ƽ��![]() ����λ���ȣ�������ƽ��m��m��0������λ���ȣ��õ��������ߣ����������ߵĶ���P����ABC�ڣ���m��ȡֵ��Χ��
����λ���ȣ�������ƽ��m��m��0������λ���ȣ��õ��������ߣ����������ߵĶ���P����ABC�ڣ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
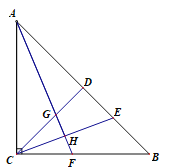
����Ŀ������Rt��ABC����DΪб��AB�ϵ��е㣬��E���߶�BD�ϣ�����CD��CE����AH��CE������ΪH����CD�ڵ�G��AH���ӳ��߽�BC�ڵ�F.
��1����֤����ADG�ա�CDE.
��2������Hǡ��ΪCE���е㣬��֤����CGF=��CFG.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����![]() �У�
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() .
.
��֤��![]() .
.
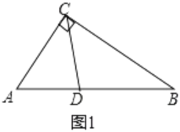
С��Ϊ��������������������˼����
��![]() ����ֱ��
����ֱ��![]() �ĶԳ�ͼ��
�ĶԳ�ͼ��![]() ����
����![]() ƽ��
ƽ��![]() ����
����![]() ������
������![]() �ϣ���
�ϣ���![]() ��
��![]() .��ˣ�Ҫ֤������ת��ΪֻҪ֤��
.��ˣ�Ҫ֤������ת��ΪֻҪ֤��![]() ����.
����.
�����С����˼����д��������������֤������.
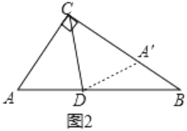
��2�����գ�1����С����˼������������������⣺
��ͼ3�����ı���![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ij�.
�ij�.
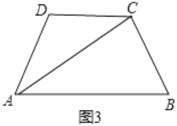
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() ��
��
![]() ��֤��ֱ��
��֤��ֱ��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
![]() ��
��![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
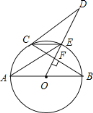
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com