
【题目】(1)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() .
.
求证:![]() .
.
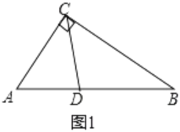
小明为解决上面的问题作了如下思考:
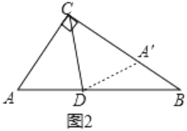
作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ,∵
,∵![]() 平分
平分![]() ,∴
,∴![]() 点落在
点落在![]() 上,且
上,且![]() ,
,![]() .因此,要证的问题转化为只要证出
.因此,要证的问题转化为只要证出![]() 即可.
即可.
请根据小明的思考,写出该问题完整的证明过程.
(2)参照(1)中小明的思考方法,解答下列问题:
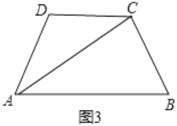
如图3,在四边形![]() 中,
中,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)21.
【解析】
(1)只需要证明![]() ,再根据等角对等边即可证明
,再根据等角对等边即可证明![]() ,再结合小明的分析即可证明;
,再结合小明的分析即可证明;
(2)作△ADC关于AC的对称图形![]() ,过点C作CE⊥AB于点E,则
,过点C作CE⊥AB于点E,则![]() =BE.设
=BE.设![]() =BE=x.在Rt△CEB和Rt△CEA中,根据勾股定理构建方程即可解决问题.
=BE=x.在Rt△CEB和Rt△CEA中,根据勾股定理构建方程即可解决问题.
解:(1)证明:如下图,作△ADC关于CD的对称图形△A′DC,
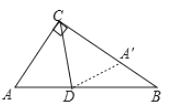
∴A′D=AD,CA′=CA,∠CA′D=∠A=60°,
∵CD平分∠ACB,
∴A′点落在CB上
∵∠ACB=90°,
∴∠B=90°-∠A=30°,
∴∠A′DB=∠CA′D-∠B=30°,即∠A′DB=∠B,
∴A′D=A′B,
∴CA+AD=CA′+A′D=CA′+A′B=CB.
(2)如图,作△ADC关于AC的对称图形△AD′C.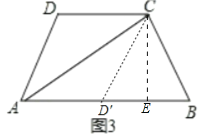
∴D′A=DA=9,D′C=DC=10,
∵AC平分∠BAD,
∴D′点落在AB上,
∵BC=10,
∴D′C=BC,
过点C作CE⊥AB于点E,则D′E=BE,
设D′E=BE=x,
在Rt△CEB中,CE2=CB2-BE2=102-x2,
在Rt△CEA中,CE2=AC2-AE2=172-(9+x)2.
∴102-x2=172-(9+x)2,
解得:x=6,
∴AB=AD′+D′E+EB=9+6+6=21.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
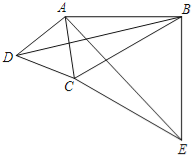
【题目】如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.
(1)求证:BD=AE;
(2)若AB=2,BC=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
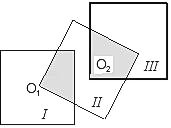
【题目】如图,有若干个边长为2的正方形,若正方形的一个顶点是正方形Ⅰ的中心O1,如图所示,类似的正方形Ⅲ的一个顶点是正方形Ⅱ的中心O2,并且正方形Ⅰ与正方形Ⅲ不重叠,如果若干个正方形都按这种方法拼接,需要m个正方形能使拼接处的图形的阴影部分的面积等于一个正方形的面积.现有一拋物线y=mx2+nx+3,其顶点在x轴上,则该抛物线的对称轴为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠B=30°,CD,CE分别是AB边上的中线和高.

(1)求证:AE=ED;
(2)若AC=2,求△CDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为营造浓厚的创建全国文明城市氛围,东营市某中学委托制衣厂制作“最美东营人”和“最美志愿者”两款文化衫.若制作“最美东营人”文化衫2件,“最美志愿者”文化衫3件,共需90元;制作“最美东营人”文化衫3件,“最美志愿者”5件,共需145元.
(1)求“最美东营人”和“最美志愿者”两款文化衫每件各多少元?
(2)若该中学要购进“最美东营人”和“最美志愿者”两款文化衫共90件,总费用少于1595元,并且“最美东营人”文化衫的数量少于“最美志愿者”文化衫的数量,那么该中学有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊿ABC中,∠B = 50,∠C = 70,AD是高,AE是角平分线,
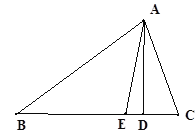
(1)∠BAC=__________,∠DAC=__________.(填度数)
(2)求∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是线段AB上的一个点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,点M,N分别是对角线AC,BE的中点,连接MN,PM,PN,若∠DAP=60°,AP2+3PB2=2,则线段MN的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com