
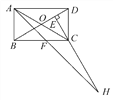
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF,EC交于点H,下列结论中:
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF,EC交于点H,下列结论中:
①AF=FH;②BO=BF;③CA=CH;④BE=3ED.其中一定成立的是________.(把所有正确结论的序号都填在横线上)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
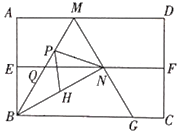
【题目】如图,四边形是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:①∠ABN= 60°;②AM=1;③![]() ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是![]() .其中正确结论的序号是___________.
.其中正确结论的序号是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在ABCD中,E、F分别是AD、BC边的中点,G、H是对角线BD上的两点,且BG=DH,则下列结论中不正确的是( )
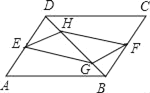
A. GF⊥FHB. GF=EH
C. EF与AC互相平分D. EG=FH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC.其中正确结论的序号是( )
EC.其中正确结论的序号是( )
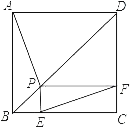
A. ①②③④B. ①②④⑤C. ②③④⑤D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某水库养殖鱼的有关情况,从该水库多个不同位置捕捞出200条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,绘制了直方图
(1)根据直方图提供的信息,这组数据的中位数落在________范围内.
(2)估计数据落在1.00~1.15中的频率是________.
(3)将上面捕捞的200条鱼分别作一记号后再放回水库.几天后再从水库的多处不同的位置捕捞150条鱼,其中带有记号的鱼有10条,请根据这一情况估算该水库中鱼的总条数.

查看答案和解析>>
科目:初中数学 来源: 题型:
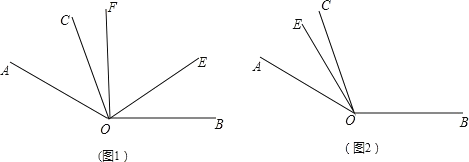
【题目】如图1,已知∠AOB=![]() ,∠AOC=
,∠AOC=![]() ,OE是∠AOB内部的一条射线,且OF平分∠AOE.
,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=![]() ,求∠COF的度数;
,求∠COF的度数;
(2)若∠COF=![]() ,求∠EOB的度数(用含n的式子表示);
,求∠EOB的度数(用含n的式子表示);
(3)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数![]() 与反比例函数
与反比例函数![]() .
.
(1)证明:直线与双曲线没有交点;
(2)若将直线![]() 向上平移4个单位后与双曲线恰好有且只有一个交点,求反比例函数的表达式和平移后的直线表达式;
向上平移4个单位后与双曲线恰好有且只有一个交点,求反比例函数的表达式和平移后的直线表达式;
(3)将(2)小题平移后的直线代表的函数记为![]() ,根据图象直接写出:对于负实数
,根据图象直接写出:对于负实数![]() ,当
,当![]() 取何值时
取何值时![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2018按一定规律排列如下表:
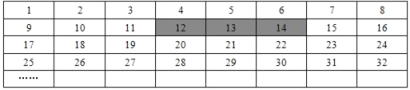
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2018 B. 2019 C. 2040 D. 2049
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com