
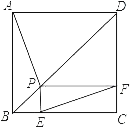
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC.其中正确结论的序号是( )
EC.其中正确结论的序号是( )
A. ①②③④B. ①②④⑤C. ②③④⑤D. ①③④⑤
【答案】B
【解析】
过P作PG⊥AB于点G,根据正方形对角线的性质及题中的已知条件,证明△AGP≌△FPE后即可证明①AP=EF;④∠PFE=∠BAP;在此基础上,根据正方形的对角线平分对角的性质,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,求得⑤DP=![]() EC.
EC.
证明:如图,过P作PG⊥AB于点G,
∵点P是正方形ABCD的对角线BD上一点,
∴GP=EP,
在△GPB中,∠GBP=45°,∴∠GPB=45°,
∴GB=GP,同理,得PE=BE,
∵AB=BC=GF,
∴AG=AB-GB,FP=GF-GP=AB-GB,
∴AG=PF,
∴△AGP≌△FPE,
①∴AP=EF;
∠PFE=∠GAP
④∴∠PFE=∠BAP,
②延长AP到EF上于一点H,
∴∠PAG=∠PFH,
∵∠APG=∠FPH,
∴∠PHF=∠PGA=90°,即AP⊥EF;
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45度,
∴当∠PAD=45度或67.5度或90度时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故③错误.
∵GF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC,
∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
⑤∴DP=![]() EC.
EC.
∴其中正确结论的序号是①②④⑤;
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个装有进水管出水管的容器,从某时刻起只打开进水管进水,经过一段时间,在打开出水管放水,至15分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(升)与时间x(分钟)之间的关系如图所示,关停进水管后,经过_____________分钟,容器中的水恰好放完.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
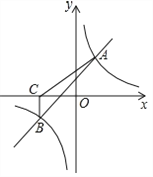
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() <
<![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桐城市发起了“保护龙眠河”行动,某学校七年级两个班的115名学生积极参与,踊跃捐款,已知甲班有![]() 的学生每人捐了10元,乙班有
的学生每人捐了10元,乙班有![]() 的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人。
的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人。
(1)用含x的代数式表示乙班人数: ;
(2)用含x的代数式表示两班捐款的总额;
(3)若x=60,则两班共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
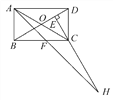
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF,EC交于点H,下列结论中:
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF,EC交于点H,下列结论中:
①AF=FH;②BO=BF;③CA=CH;④BE=3ED.其中一定成立的是________.(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=24,动点P从A出发,以每秒2个单位的速度沿射线AB运动,运动时间为t秒(t>0),点M为AP的中点.
![]()
(1)当点P在线段AB上运动时.当t为多少时,AM=6.
(2)当点P在AB延长线上运动时,点N为BP的中点,求出线段MN的长度.
(3)在P点的运动过程中,点N为BP的中点,是否存在这样的t的值,使M、N、B三点中的一个点是以其余两点为端点的线段的中点,若有,请求出t的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知轮船在静水中航行的速度是m千米/时,水流的速度是a千米/时.
(1)轮船顺水航行的速度为 km/h,轮船逆流航行的速度为 km/h.
(2)若轮船顺水航行3小时,逆水航行2小时,则轮船共航行多少千米?
(3)当m=80,a=3时,则轮船共航行多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
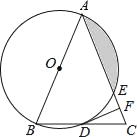
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E.过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com