
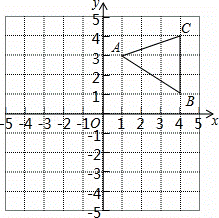
如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
(1)请按要求画图:
①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
(2)请写出直线B1C1与直线B2C2的交点坐标.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=( )
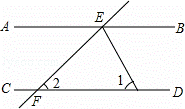
A. 64° B. 63° C. 60° D. 54°
查看答案和解析>>
科目:初中数学 来源: 题型:
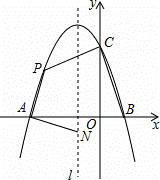
如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴I为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴I上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
某动车站在原有的普通售票窗口外新增了无人售票窗口,普通售票窗口从上午8点开放,而无人售票窗口从上午7点开放, 某日从上午7点到10点,每个普通售票窗口售出的车票数
某日从上午7点到10点,每个普通售票窗口售出的车票数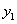 (张)与售票时
(张)与售票时 间x(小时)的
间x(小时)的 变化趋势如图1,每个无人售票窗口售出的车票数
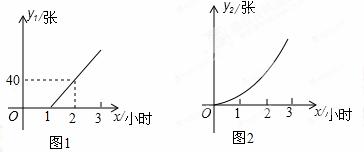
变化趋势如图1,每个无人售票窗口售出的车票数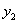 (张)与售票时间x(小时)的变化趋势是以原点为顶点的抛物线的一部分,如图2,若该日截至上午9点,每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同.
(张)与售票时间x(小时)的变化趋势是以原点为顶点的抛物线的一部分,如图2,若该日截至上午9点,每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同.
(1)求图2中所确定抛物线的解析式;
(2)若该日共开放5个无人售票窗口,截至上午10点,两种窗口共售出的车票数不少于900张,则至少需要开放多少个普通售票窗口?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、CD于M、N两点.若AM=2,则线段ON的长为( )
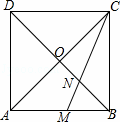
A. B. C. 1 D. 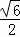
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com