
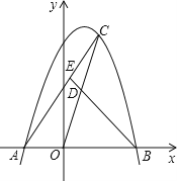
【题目】如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A、B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A、B不重合),D是OC的中点,连接BD并延长,交AC于点E.
(1)用含m的代数式表示点A、B的坐标;
(2)求证:![]() ;
;
(3)若点C、点A到y轴的距离相等,且s△CDE=1.6时,求抛物线和直线BE的解析式.
【答案】(1)A(-m,0),b(2m,0);(2)见解析;(3)y=-x2+2x+8,![]()
【解析】
(1)解x的方程-x2+mx+2m2=0,x1=-m,x2=2m.因为点A在点B的左边,且m>0,所以A(-m,0),b(2m,0);
(2)过点O作OG//AC交BE于点G.则△CED∽△OGD,所以![]() ; 由△BOG∽△BAE,得
; 由△BOG∽△BAE,得![]() .因为OB=2m,AB=3m,代入可求出结论;
.因为OB=2m,AB=3m,代入可求出结论;
(3)连接OE,易得S△OCE=2S△CED,因为![]() ,所以
,所以![]() ,即S△AOC=5S△CED=8,点C(m,2m2),由S△AOC=
,即S△AOC=5S△CED=8,点C(m,2m2),由S△AOC=![]() OA|yC|=
OA|yC|=![]() 求得m=2.进而可求出抛物线的解析式和直线BE的解析式.
求得m=2.进而可求出抛物线的解析式和直线BE的解析式.
解:(1)∵抛物线y=-x2+mx+2m2(m>0)与x轴交于A、B两点,
∴关于x的方程-x2+mx+2m2=0有两个不相等的实数根x1和x2;
解得x1=-m,x2=2m.
∵点A在点B的左边,且m>0,
∴A(-m,0),b(2m,0);
(2)过点O作OG∥AC交BE于点G.
∴△CED∽△OGD,∴![]() ;
;
∵DC=DO,
∴CE=OG;
∵OG//AC,
∴△BOG∽△BAE,∴![]() .
.
∵OB=2m,AB=3m,
∴![]() .
.
(3)连接OE.
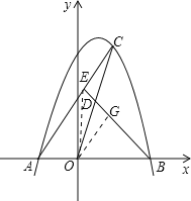
∵D是OC的中点,
∴S△OCE=2S△CED,
∵![]() ,∴
,∴![]() ,∴S△AOC=5S△CED=8,
,∴S△AOC=5S△CED=8,
∵点C、点A到y轴的距离相等,点C在抛物线y=-x2+mx+2m2上,
∴点C(m,2m2),
∵S△AOC=![]() OA|yC|=
OA|yC|= ![]() =
=![]() ,
,
∴m3=8,解得m=2.
∴抛物线的解析式为y=-x2+2x+8,
∴点B(4,0),点C(2,8).
∴此时D为(1,4),
设直线BE的解析式为:y=kx+b,
∴![]() ,
,
解得
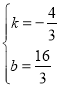 ,
,
∴直线BE的解析式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于原点
轴交于原点![]() 和点
和点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)求抛物线的表达式,并写出它的对称轴;
(2)求![]() 的值;
的值;
(3)点![]() 在抛物线的对称轴上,如果
在抛物线的对称轴上,如果![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
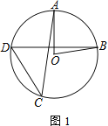
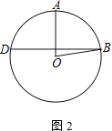
【题目】如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1) 若点C在优弧BD上,求∠ACD的大小
(2) 若点C在劣弧BD上,直接写出∠ACD的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=2.
(1)试在图中画出将△ABC以B为旋转中心,沿顺时针方向旋转90°后的图形△A1BC1;
(2)若点B的坐标为(-1,-4),点C的坐标为(-3,-4),试在图中画出直角坐标系,并写出点A的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型加工厂准备每天生产甲、乙两种类型的产品共1000件,原料成本、销售单价,及工人计件工资如表:
甲(元/件) | 乙(元/件) | |
原料成本 | 10 | 8 |
销售单价 | 20 | 16 |
计件工资 | 2 | 1.5 |
设该加工厂每天生产甲型产品x件,每天获得总利润为y元.
(1)求出y与x之间的函数关系式;
(2)若该工厂每天投人总成本不超过10750元,怎样安排甲、乙两种类型的生产量,可使该厂每天所获得的利润最大?并求出最大利润.(总成本=原料成本+计件工资,利润=销售收入一投人总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店用1200元购进了A、B两种羽毛球拍.已知A种羽毛球拍进价为每副12元,B种羽毛球拍进价为每副10元.文教店在销售时A种羽毛球拍售价为每副15元,B种羽毛球拍售价为每副12元,全部售完后共获利270元.
(1)求这个文教店购进A、B两种羽毛球拍各多少副?
(2)若该文教店以原进价再次购进A、B两种羽毛球拍,且购进A种羽毛球拍的数量不变,而购进B种羽毛球拍的数量是第一次的2倍,B种羽毛球拍按原售价销售,而A种羽毛球拍降价销售.当两种羽毛球拍销售完毕时,要使再次购进的羽毛球拍获利不少于340元,A种羽毛球拍最低售价每副应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
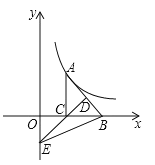
【题目】如图,点A是反比例函数y=![]() (k>0,x>0)图象上一点,B、C在x轴上,且AC⊥BC,D为AB的中点,DC的延长线交y轴于E,连接BE,若△BCE的面积为8,则k的值为_____.
(k>0,x>0)图象上一点,B、C在x轴上,且AC⊥BC,D为AB的中点,DC的延长线交y轴于E,连接BE,若△BCE的面积为8,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象都经过点A(m,2).
)的图象都经过点A(m,2).

(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数![]() 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com