
【题目】某小型加工厂准备每天生产甲、乙两种类型的产品共1000件,原料成本、销售单价,及工人计件工资如表:
甲(元/件) | 乙(元/件) | |
原料成本 | 10 | 8 |
销售单价 | 20 | 16 |
计件工资 | 2 | 1.5 |
设该加工厂每天生产甲型产品x件,每天获得总利润为y元.
(1)求出y与x之间的函数关系式;
(2)若该工厂每天投人总成本不超过10750元,怎样安排甲、乙两种类型的生产量,可使该厂每天所获得的利润最大?并求出最大利润.(总成本=原料成本+计件工资,利润=销售收入一投人总成本)
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步面见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为多少步.

查看答案和解析>>
科目:初中数学 来源: 题型:
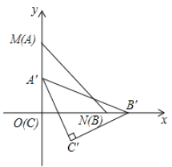
【题目】如图,已知点![]() ,开始时,
,开始时,![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 分别与点
分别与点![]() 、
、![]() 、
、![]() 重合,点
重合,点![]() 在
在![]() 轴上从点
轴上从点![]() 开始向点
开始向点![]() 滑动,到达点
滑动,到达点![]() 结束运动,同时点
结束运动,同时点![]() 沿着
沿着![]() 轴向右滑动,则在此运动过程中,点
轴向右滑动,则在此运动过程中,点![]() 的运动路径长为_______.
的运动路径长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
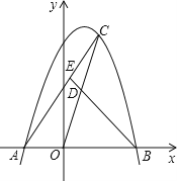
【题目】如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A、B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A、B不重合),D是OC的中点,连接BD并延长,交AC于点E.
(1)用含m的代数式表示点A、B的坐标;
(2)求证:![]() ;
;
(3)若点C、点A到y轴的距离相等,且s△CDE=1.6时,求抛物线和直线BE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边与正方形CGFE的边CE重合,O是EG的中点,![]() 的平分线GH过点D,交BE于点H,连接OH、FH,EG与FH交于点M,对于下面四个结论:①
的平分线GH过点D,交BE于点H,连接OH、FH,EG与FH交于点M,对于下面四个结论:①![]() ;②
;②![]() //且=
//且=![]() ;③
;③![]() ;④
;④![]() ∽
∽![]() ,其中正确的有( )
,其中正确的有( )
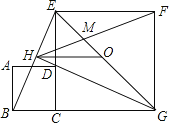
A.1个B.2个C. 3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
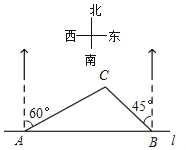
【题目】如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于_____千米.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,延长CO交AB于点D,记∠A=![]() ,∠ABC=β.
,∠ABC=β.
(1)求∠ADC的度数(用含α、β的式子表示);
(2)过点C作CE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F,CE,BF相交于点G,取![]() 中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.
中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
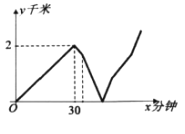
【题目】周末小明匀速步行赶往学校参加学校组织的植树活动,小明从家出发30分钟后,忽然想起没有带植树工具,于是马上掉头往回走行走速度比之前提高了1千米/时(仍保持匀速步行),同时小明打电话给爸爸,请爸爸帮他把植树工具送过来,从小明开始打电话到爸爸出门一共用了4分钟,爸爸的行走速度与此时小明的行走速度相同,两人相遇后,小明立即赶往学校,爸爸则转身回家,两人速度均保持不变,爸爸在回家途中用了10分钟吃早餐,然后立即回家,当爸爸到家时小明刚好到达学校.爸爸和小明相距的路程y(千米)与小明从家出发的时间x(分钟)之间的关系如图所示,求今天早上小明从家到学校途中行走的总路程是________千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com