
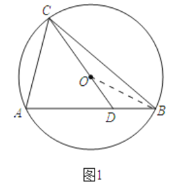
【题目】如图,已知△ABC内接于⊙O,延长CO交AB于点D,记∠A=![]() ,∠ABC=β.
,∠ABC=β.
(1)求∠ADC的度数(用含α、β的式子表示);
(2)过点C作CE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F,CE,BF相交于点G,取![]() 中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.
中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.

【答案】(1)![]() ;(2)①证明见解析;②证明见解析.
;(2)①证明见解析;②证明见解析.
【解析】
(1)根据∠CDA=∠DCB+∠ABC,只要求出∠DCB即可解决问题.
(2)①延长CD交⊙O于T,连接BT,OH.根据CT是直径,可得∠AEC=∠BFC=∠CBT=90°,根据等量关系可得∠FCG=∠BCT,然后可得△CFG∽△CBT,根据α+β=120°可得∠ACB=60°,然后求出∠CBF=30°,根据相似的性质求出CG=![]() CT =CO;
CT =CO;
②根据垂弦定理得出OH⊥AB,已知CE⊥AB,可得CG∥OH,推出四边形CGHO是平行四边形即可解决问题.
(1)解:如图1中,连接OB,
∵∠BOC=2∠A=2![]() ,OC=OB,
,OC=OB,
∴∠OCB=![]() (180°-2
(180°-2![]() )=90°-
)=90°-![]() ,
,
∴∠ADC=∠OCB+∠ABC=![]() .
.
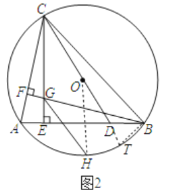
(2)证明:如图2,延长CD交⊙O于T,连接BT,OH.
①∵CT是直径,
∴∠CBT=90°,
∵CE⊥AB,BF⊥AC,
∴∠AEC=∠BFC=∠CBT=90°,
∴∠A+∠ACE=90°,∠T+∠BCT=90°,
∵∠A=∠T,
∴∠FCG=∠BCT,
∵α+β=120°,
∴∠ACB=60°,
∴∠CBF=30°,
∴BC=2CF,
∵∠FCG=∠BCT,∠CFG=∠CBT=90°,
∴△CFG∽△CBT,
∴![]() =2,
=2,
∴CG=![]() CT=OC=OT=OH,
CT=OC=OT=OH,
②∵![]() ,
,
∴OH⊥AB,
∵CE⊥AB,
∴CE∥OH,∵CG=OH,
∴四边形CGHO是平行四边形,
∴GH∥CD.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
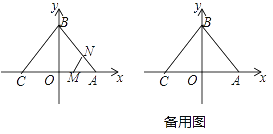
【题目】如图,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(-3,0).动点M,N同时从A点出发,M沿A→C,N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动时间记为t秒.连接MN.
(1)求直线BC的解析式;
(2)移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;
(3)当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小型加工厂准备每天生产甲、乙两种类型的产品共1000件,原料成本、销售单价,及工人计件工资如表:
甲(元/件) | 乙(元/件) | |
原料成本 | 10 | 8 |
销售单价 | 20 | 16 |
计件工资 | 2 | 1.5 |
设该加工厂每天生产甲型产品x件,每天获得总利润为y元.
(1)求出y与x之间的函数关系式;
(2)若该工厂每天投人总成本不超过10750元,怎样安排甲、乙两种类型的生产量,可使该厂每天所获得的利润最大?并求出最大利润.(总成本=原料成本+计件工资,利润=销售收入一投人总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别在△ABC的边AC、AB上,延长DE、CB交于点F,且AEAB=ADAC.
(1)求证:∠FEB=∠C;
(2)连接AF,若![]() ,求证:EFAB=ACFB.
,求证:EFAB=ACFB.

查看答案和解析>>
科目:初中数学 来源: 题型:
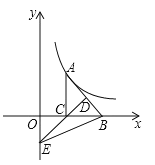
【题目】如图,点A是反比例函数y=![]() (k>0,x>0)图象上一点,B、C在x轴上,且AC⊥BC,D为AB的中点,DC的延长线交y轴于E,连接BE,若△BCE的面积为8,则k的值为_____.
(k>0,x>0)图象上一点,B、C在x轴上,且AC⊥BC,D为AB的中点,DC的延长线交y轴于E,连接BE,若△BCE的面积为8,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察发现:如图1,在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,过
上,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() .填空:
.填空:
①![]() 与
与![]() 是否相似(直接回答)________;
是否相似(直接回答)________;
②![]() ________;
________;![]() ________;
________;
(2)拓展探究:将![]() 绕顶点
绕顶点![]() 旋转到图2所示的位置,猜想
旋转到图2所示的位置,猜想![]() 与
与![]() 是否相似?若不相似,说明理由;若相似,请证明;
是否相似?若不相似,说明理由;若相似,请证明;
(3)迁移应用:将![]() 绕顶点
绕顶点![]() 旋转到点
旋转到点![]() 、
、![]() 、
、![]() 在同一条直线上时,直接写出线段
在同一条直线上时,直接写出线段![]() 的长.
的长.
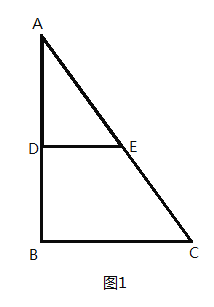


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC边长为2,D为BC中点,连接AD.点O在线段AD上运动(不含端点A、D),以点O为圆心,![]() 长为半径作圆,当
长为半径作圆,当![]() O与△ABC的边有且只有两个公共点时,DO的取值范围为_____.
O与△ABC的边有且只有两个公共点时,DO的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
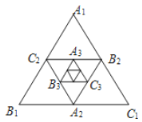
【题目】如图,小红作出了边长为1的第1个正三角形![]() ,算出了正
,算出了正![]() 的面积,然后分别取
的面积,然后分别取![]() 三边的中点
三边的中点![]() ,作出了第二个正三角形
,作出了第二个正三角形![]() ,算出第2个正
,算出第2个正![]() 的面积,用同样的方法作出了第3个正
的面积,用同样的方法作出了第3个正![]() ,算出第3个正
,算出第3个正![]() 的而积,依此方法作下去,由此可得第
的而积,依此方法作下去,由此可得第![]() 个作出的正
个作出的正![]() 的面积是______
的面积是______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com