
【题目】如图,点D、E分别在△ABC的边AC、AB上,延长DE、CB交于点F,且AEAB=ADAC.
(1)求证:∠FEB=∠C;
(2)连接AF,若![]() ,求证:EFAB=ACFB.
,求证:EFAB=ACFB.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场销售A、B两种品牌的教学设备,其进价分别为![]() 万元
万元![]() 套,
套,![]() 万元
万元![]() 套;售价分别为
套;售价分别为![]() 万元
万元![]() 套、
套、![]() 万元
万元![]() 套.该商场计划购进两种教学设备各若干套,共需66万元,全部销售后可获毛利润9万元.
套.该商场计划购进两种教学设备各若干套,共需66万元,全部销售后可获毛利润9万元.
(1)设该商场计划购进A、B两种品牌的教学设备各x套、y套,求x,y的值.
(2)调研后,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的![]() 倍,采购进资金不超过69万元,问A种设备购进量至多减少多少套?
倍,采购进资金不超过69万元,问A种设备购进量至多减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边与正方形CGFE的边CE重合,O是EG的中点,![]() 的平分线GH过点D,交BE于点H,连接OH、FH,EG与FH交于点M,对于下面四个结论:①
的平分线GH过点D,交BE于点H,连接OH、FH,EG与FH交于点M,对于下面四个结论:①![]() ;②
;②![]() //且=
//且=![]() ;③
;③![]() ;④
;④![]() ∽
∽![]() ,其中正确的有( )
,其中正确的有( )
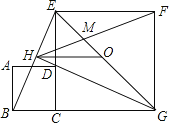
A.1个B.2个C. 3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
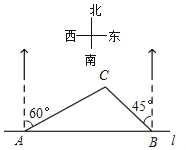
【题目】如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于_____千米.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民的生活水平的不断提高,学生身边的零用钱也多了.夏雪同学调查了班级同学身上有多少零用钱,将每位同学的零用钱记录下来,下面是全班40名同学的零用钱的数目(单位:元)
2,5,0,5,2,5,6,5,0,5,5,5,2,5,8,0,5,5,2,5,
5,8,6,5,2,5,5,2,5,6,5,5,0,6,5,6,5,2,5,0.
(1)请你写出同学的零用钱(0元,2元,5元,6元8元)出现的频数;
(2)求出同学的零用钱的平均数、中位数和众数;
(3)假如老师随机问一个同学的零用钱,老师最有可能得到的回答是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,延长CO交AB于点D,记∠A=![]() ,∠ABC=β.
,∠ABC=β.
(1)求∠ADC的度数(用含α、β的式子表示);
(2)过点C作CE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F,CE,BF相交于点G,取![]() 中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.
中点H,连接GH.若α+β=120°,求证:①CG=CO;②GH∥CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长。
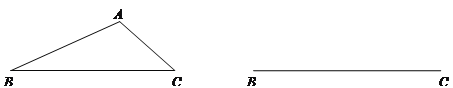
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com