
ЁОЬтФПЁПФГЩЬГЁЯњЪлAЁЂBСНжжЦЗХЦЕФНЬбЇЩшБИЃЌЦфНјМлЗжБ№ЮЊ![]() ЭђдЊ
ЭђдЊ![]() ЬзЃЌ
ЬзЃЌ![]() ЭђдЊ
ЭђдЊ![]() ЬзЃЛЪлМлЗжБ№ЮЊ
ЬзЃЛЪлМлЗжБ№ЮЊ![]() ЭђдЊ
ЭђдЊ![]() ЬзЁЂ
ЬзЁЂ![]() ЭђдЊ
ЭђдЊ![]() ЬзЃЎИУЩЬГЁМЦЛЎЙКНјСНжжНЬбЇЩшБИИїШєИЩЬзЃЌЙВаш66ЭђдЊЃЌШЋВПЯњЪлКѓПЩЛёУЋРћШѓ9ЭђдЊЃЎ
ЬзЃЎИУЩЬГЁМЦЛЎЙКНјСНжжНЬбЇЩшБИИїШєИЩЬзЃЌЙВаш66ЭђдЊЃЌШЋВПЯњЪлКѓПЩЛёУЋРћШѓ9ЭђдЊЃЎ
ЃЈ1ЃЉЩшИУЩЬГЁМЦЛЎЙКНјAЁЂBСНжжЦЗХЦЕФНЬбЇЩшБИИїxЬзЁЂyЬзЃЌЧѓxЃЌyЕФжЕЃЎ
ЃЈ2ЃЉЕїбаКѓЃЌИУЩЬГЁОіЖЈдкдМЦЛЎЕФЛљДЁЩЯЃЌМѕЩйAжжЩшБИЕФЙКНјЪ§СПЃЌдіМгBжжЩшБИЕФЙКНјЪ§СПЃЌвбжЊBжжЩшБИдіМгЕФЪ§СПЪЧAжжЩшБИМѕЩйЪ§СПЕФ![]() БЖЃЌВЩЙКНјзЪН№ВЛГЌЙ§69ЭђдЊЃЌЮЪAжжЩшБИЙКНјСПжСЖрМѕЩйЖрЩйЬзЃП
БЖЃЌВЩЙКНјзЪН№ВЛГЌЙ§69ЭђдЊЃЌЮЪAжжЩшБИЙКНјСПжСЖрМѕЩйЖрЩйЬзЃП
ЁОД№АИЁПЃЈ1ЃЉAЃЌBСНжжЦЗХЦЗжБ№ЮЊ20ЬзЃЌ30ЬзЃЛЃЈ2ЃЉ10ЬзЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтЪзЯШЩшИУЩЬГЁМЦЛЎЙКНјAЃЌBСНжжЦЗХЦЕФНЬбЇЩшБИЗжБ№ЮЊxЬзЃЌyЬзЃЌИљОнЬтвтМДПЩСаЗНГЬзщ![]() ЃЌНтДЫЗНГЬзщМДПЩЧѓЕУД№АИЃЛ
ЃЌНтДЫЗНГЬзщМДПЩЧѓЕУД№АИЃЛ
ЃЈ2ЃЉИљОнЬтвтЪзЯШЩшAжжЩшБИЙКНјЪ§СПМѕЩйaЬзЃЌдђBжжЩшБИЙКНјЪ§СПдіМг![]() ЬзЃЌИљОнЬтвтМДПЩСаВЛЕШЪН
ЬзЃЌИљОнЬтвтМДПЩСаВЛЕШЪН![]() ЃЌНтДЫВЛЕШЪНзщМДПЩЧѓЕУД№АИЃЎ
ЃЌНтДЫВЛЕШЪНзщМДПЩЧѓЕУД№АИЃЎ
НтЃКЃЈ1ЃЉЩшИУЩЬГЁМЦЛЎЙКНјAЃЌBСНжжЦЗХЦЕФНЬбЇЩшБИЗжБ№ЮЊxЬзЃЌyЬзЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
Д№ЃКИУЩЬГЁМЦЛЎЙКНјAЃЌBСНжжЦЗХЦЕФНЬбЇЩшБИЗжБ№ЮЊ20ЬзЃЌ30ЬзЃЛ
ЃЈ2ЃЉЩшAжжЩшБИЙКНјЪ§СПМѕЩйaЬзЃЌдђBжжЩшБИЙКНјЪ§СПдіМг![]() ЬзЃЌ
ЬзЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
Д№ЃКAжжЩшБИЙКНјЪ§СПжСЖрМѕЩй10ЬзЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮABCDЕФБпГЄЮЊ3ЃЌEЁЂFЗжБ№ЪЧABЁЂBCБпЩЯЕФЕу,ЧвЁЯEDF=45Ёу.НЋЁїDAEШЦЕуDФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїDCM.
ЃЈ1ЃЉЧѓжЄЃКEF=FM
ЃЈ2ЃЉЕБAE=1ЪБЃЌЧѓEFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
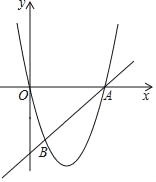
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпABгыХзЮяЯпyЃНax2+bxНЛгкЕуAЃЈ6ЃЌ0ЃЉКЭЕуBЃЈ1ЃЌЉ5ЃЉЃЎ
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЕФБэДяЪНКЭжБЯпABЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћЕуCдкжБЯпABЩЯЃЌЧвЁЯBOCЕФе§ЧажЕЪЧ![]() ЃЌЧѓЕуCЕФзјБъЃЎ
ЃЌЧѓЕуCЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
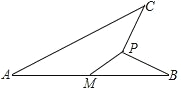
ЁОЬтФПЁПШчЭМЃЌЯпЖЮ ABЃН4ЃЌM ЮЊ AB ЕФжаЕуЃЌЖЏЕу P ЕНЕу M ЕФОрРыЪЧ 1ЃЌСЌНг PBЃЌЯпЖЮ
PB ШЦЕу P ФцЪБеыа§зЊ 90ЁуЕУЕНЯпЖЮ PCЃЌСЌНг ACЃЌдђЯпЖЮ AC ГЄЖШЕФзюДѓжЕЪЧ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
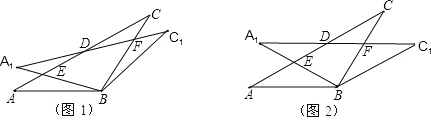
ЁОЬтФПЁПдкЁїABC жаЃЌAB=BC=2ЃЌЁЯABC=120ЁуЃЌНЋЁїABC ШЦЕу B ЫГЪБеыа§зЊНЧІСЃЈ0ЁуЃМІСЃМ90ЁуЃЉЕУЁїA1BC1ЃЌA1B НЛ AC гкЕу EЃЌA1C1 ЗжБ№НЛ ACЁЂBC гк DЁЂF СНЕуЃЎ
ЃЈ1ЃЉШчЭМ 1ЃЌЙлВьВЂВТЯыЃЌдка§зЊЙ§ГЬжаЃЌЯпЖЮ EA1 гы FC гадѕбљЕФЪ§СПЙиЯЕЃП ВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉШчЭМ 2ЃЌЕБІС=30ЁуЪБЃЌЪдХаЖЯЫФБпаЮ BC1DA ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧщПіЯТЃЌЧѓ ED ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
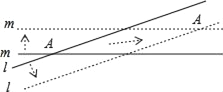
ЁОЬтФПЁПИљОнАЎвђЫЙЬЙЕФЯрЖдТлПЩжЊЃЌШЮКЮЮяЬхЕФдЫЖЏЫйЖШВЛФмГЌЙ§ЙтЫйЃЈ3ЁС105km/sЃЉЃЌвђЮЊвЛИіЮяЬхДяЕНЙтЫйашвЊЮоЧюЖрЕФФмСПЃЌВЂЧвЪБЙтЛсЕЙСїЃЌетдкЯжЪЕжаЪЧВЛПЩФмЕФЃЎЕЋЮвУЧПЩШУвЛИіащФтЮяГЌЙтЫйдЫЖЏЃЌР§ШчЃКжБЯпlЃЌmБэЪОСНЬѕФОАєЯрНЛГЩЕФШёНЧЕФЖШЪ§ЮЊ10ЁуЃЌЫќУЧЗжБ№вдгыздЩэДЙжБЕФЗНЯђЯђСНВрЦНвЦЪБЃЌЫќУЧЕФНЛЕуAвВЫцзХвЦЖЏЃЈШчЭММ§ЭЗЫљЪОЃЉЃЌШчЙћСНЬѕжБЯпЕФвЦЖЏЫйЖШЖМЪЧЙтЫйЕФ0.2БЖЃЌдђНЛЕуAЕФвЦЖЏЫйЖШЪЧЙтЫйЕФ_____БЖЃЎЃЈНсЙћБЃСєСНИігааЇЪ§зжЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
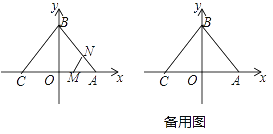
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЕФЖЅЕузјБъЗжБ№ЮЊAЃЈ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌCЃЈ-3ЃЌ0ЃЉ.ЖЏЕуMЃЌNЭЌЪБДгAЕуГіЗЂЃЌMбиAЁњC,NбиелЯпAЁњBЁњCЃЌОљвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШвЦЖЏЃЌЕБвЛИіЖЏЕуЕНДяжеЕуCЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙвЦЖЏЃЌвЦЖЏЪБМфМЧЮЊtУы.СЌНгMN.
ЃЈ1ЃЉЧѓжБЯпBCЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвЦЖЏЙ§ГЬжаЃЌНЋЁїAMNбижБЯпMNЗелЃЌЕуAЧЁКУТфдкBCБпЩЯЕуDДІЃЌЧѓДЫЪБtжЕМАЕуDЕФзјБъЃЛ
ЃЈ3ЃЉЕБЕуM,NвЦЖЏЪБЃЌМЧЁїABCдкжБЯпMNгвВрВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЪБМфtЕФКЏЪ§ЙиЯЕЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
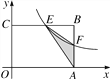
ЁОЬтФПЁПШчЭМЃЌдкОиаЮOABCжаЃЌOAЃН3ЃЌOCЃН2ЃЌFЪЧABЩЯЕФвЛИіЖЏЕу(FВЛгыAЃЌBжиКЯ)ЃЌЙ§ЕуFЕФЗДБШР§КЏЪ§yЃН![]() (xЃО0)ЕФЭМЯѓгыBCБпНЛгкЕуE.
(xЃО0)ЕФЭМЯѓгыBCБпНЛгкЕуE.
(1)ЕБFЮЊABЕФжаЕуЪБЃЌЧѓИУКЏЪ§ЕФНтЮіЪНЃЛ
(2)ЕБkЮЊКЮжЕЪБЃЌЁїEFAЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуDЁЂEЗжБ№дкЁїABCЕФБпACЁЂABЩЯЃЌбгГЄDEЁЂCBНЛгкЕуFЃЌЧвAEABЃНADACЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯFEBЃНЁЯCЃЛ
ЃЈ2ЃЉСЌНгAFЃЌШє![]() ЃЌЧѓжЄЃКEFABЃНACFBЃЎ
ЃЌЧѓжЄЃКEFABЃНACFBЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com