
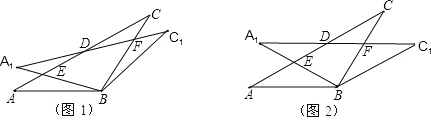
【题目】在△ABC 中,AB=BC=2,∠ABC=120°,将△ABC 绕点 B 顺时针旋转角α(0°<α<90°)得△A1BC1,A1B 交 AC 于点 E,A1C1 分别交 AC、BC 于 D、F 两点.
(1)如图 1,观察并猜想,在旋转过程中,线段 EA1 与 FC 有怎样的数量关系? 并证明你的结论;
(2)如图 2,当α=30°时,试判断四边形 BC1DA 的形状,并说明理由;
(3)在(2)的情况下,求 ED 的长.
【答案】(1)EA1=FC.证明见解析;(2)四边形 BC1DA 是菱形.证明见解析;(3)ED=2-![]() .
.
【解析】
(1)根据旋转的性质得到对应边相等和对应角相等,从而得到全等三角形,根据全等三角形的性质进行证明;
(2)在(1)的基础上,易发现该四边形的四条边相等,从而证明是菱形;
(3)根据菱形的性质和解直角三角形的知识以及等腰三角形的性质求解.
(1)EA1=FC.
证明:∵AB=BC,
∴∠A=∠C.
由旋转可知,AB=BC1,∠A=∠C1,∠ABE=∠C1BF,
∴△ABE≌△C1BF.
∴BE=BF,又∵BA1=BC,
∴BA1﹣BE=BC﹣BF.即 EA1=FC.
(2)四边形 BC1DA 是菱形.
证明:∵∠A1=∠ABA1=30°,
∴A1C1∥AB,同理 AC∥BC1.
∴四边形 BC1DA 是平行四边形. 又∵AB=BC1,
∴四边形 BC1DA 是菱形.
(3)过点E作EG⊥AB于点G,则AG=BG=1.

在Rt△AEG中,AE=![]() .
.
由(2)知四边形BC1DA是菱形,
∴AD=AB=2,
∴ED=AD-AE=2-![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
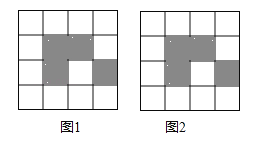
【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数![]() 的图象,下列结论错误的是( )
的图象,下列结论错误的是( )
A.图象经过一、二、四象限
B.与![]() 轴的交点坐标为
轴的交点坐标为![]()
C.![]() 随
随![]() 的增大而减小
的增大而减小
D.图象与两坐标轴相交所形成的直角三角形的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让“两会”精神深入青年学生,增强学子们的历史使命和社会责任感,某高校党委举办了“奋力奔跑同心追梦”两会主题知识竞答活动,文学社团为选派优秀同学参加学校竞答活动,提前对甲、乙两位同学进行了6次测验:
①收集数据:分别记录甲、乙两位同学6次测验成绩(单位:分)
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
②整理数据:列表格整理两位同学的测验成绩(单位:分)
1 | 2 | 3 | 4 | 5 | 6 | |
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
③描述数据:根据甲、乙两位同学的成绩绘制折线统计图

④分析数据:两组成绩的平均数、中位数、众数、方差如下表:
同学 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 84 | 82.5 | __________ | 16.3 |
乙 | 84 | 83.5 | 83 | __________ |
得出结论:结合上述统计过程,回答下列问题:
(1)补全④中表格;
(2)甲、乙两名同学中,_______(填甲或乙)的成绩更稳定,理由是______________________
(3)如果由你来选择一名同学参加学校的竞答活动,你会选择__________(填甲或乙),理由是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
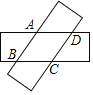
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴交于A(﹣2,0)、B(4,0)两点,且函数经过点(3,10).
(1)求二次函数的解析式;
(2)设这个二次函数的顶点为P,求△ABP的面积;
(3)当x为何值时,y≤0.(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的含30°角的三角尺按如图1所示的方式摆放在一起,它们较短的直角边BC=EC=3.
(1)将△ECD沿直线l向左平移到图2的位置,使点E′落在AB上,则CC′= ;
(2)将△ECD绕点C逆时针旋转到图3的位置,使点E′落在AB上,则△ECD绕点C旋转的度数为 ;
(3)将△ECD沿直线AC翻折到图4的位置,ED′与AB相交于点F,求证:AF=FD′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(﹣![]() ,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com