
【题目】将两块全等的含30°角的三角尺按如图1所示的方式摆放在一起,它们较短的直角边BC=EC=3.
(1)将△ECD沿直线l向左平移到图2的位置,使点E′落在AB上,则CC′= ;
(2)将△ECD绕点C逆时针旋转到图3的位置,使点E′落在AB上,则△ECD绕点C旋转的度数为 ;
(3)将△ECD沿直线AC翻折到图4的位置,ED′与AB相交于点F,求证:AF=FD′.

【答案】(1)3﹣![]() ;(2)30°;(3)见解析
;(2)30°;(3)见解析
【解析】
(1)先判断出C'E'=3,再利用含30度角的直角三角形的性质得出BE'=2BC,最后用勾股定理求出BC'即可得出结论;
(2)△ECD绕点C旋转的度数即∠ECE'的度数;易得:∠ECE′=∠BAC=30°;
(3)根据条件,证明△AEF≌△D′BF进而得出AF=FD′.
解:(1)解:CC′=3﹣![]() .
.
理由如下:由平移知,C'E'∥AC,C'E'=CE=3,
∴∠BE'C'=∠A=30°,
∵BC=EC=3,
在Rt△BC'E'中,∠BE'C'=30°,
根据在直角三角形中,30°角所对的直角边是斜边的一半,得BE'=2BC'
∴BE'2﹣BC'2=C'E'2,
即:4BC'2﹣BC'2=9,
∴BC'=![]() ,
,
∴CC′=BC﹣BC'=3﹣![]() ;
;
故答案为:3﹣![]() ;
;
(2)解:△ECD绕点C旋转的度数即∠ECE′的度数;
∵∠ABC=60°,BC=CE′=3,AB=6,
∴△E′BC是等边三角形,
∴BC=E′C=E′B=3,
∴AE′=E′C=3,
∴∠E′AC=∠E′CA,
∴∠ECE′=∠BAC=30°;
故答案为:30°;
(3)证明:∵AE=AC﹣EC,D′B=D′C﹣BC,
又∵AC=D′C,EC=BC,
∴AE=D′B,
又∵∠AEF=∠D′BF=180°﹣60°=120°,∠A=∠CD′E=30°,
在△AEF和△D′BF中,
 ,
,
∴△AEF≌△D′BF(ASA),
∴AF=FD'.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】(问题背景)如图1所示,在![]() 中,
中,![]() ,
,![]() ,点D为直线
,点D为直线![]() 上的个动点(不与B、C重合),连结
上的个动点(不与B、C重合),连结![]() ,将线段
,将线段![]() 绕点D按顺时针方向旋转90°,使点A旋转到点E,连结
绕点D按顺时针方向旋转90°,使点A旋转到点E,连结![]() .
.
(问题初探)如果点D在线段![]() 上运动,通过观察、交流,小明形成了以下的解题思路:过点E作
上运动,通过观察、交流,小明形成了以下的解题思路:过点E作![]() 交直线
交直线![]() 于F,如图2所示,通过证明
于F,如图2所示,通过证明![]() ______,可推证
______,可推证![]() 是_____三角形,从而求得
是_____三角形,从而求得![]() ______°.
______°.
(继续探究)如果点D在线段![]() 的延长线上运动,如图3所示,求出
的延长线上运动,如图3所示,求出![]() 的度数.
的度数.
(拓展延伸)连接![]() ,当点D在直线
,当点D在直线![]() 上运动时,若
上运动时,若![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
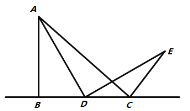
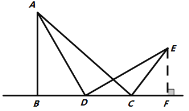
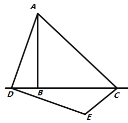
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
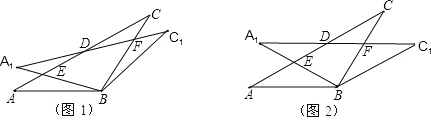
【题目】在△ABC 中,AB=BC=2,∠ABC=120°,将△ABC 绕点 B 顺时针旋转角α(0°<α<90°)得△A1BC1,A1B 交 AC 于点 E,A1C1 分别交 AC、BC 于 D、F 两点.
(1)如图 1,观察并猜想,在旋转过程中,线段 EA1 与 FC 有怎样的数量关系? 并证明你的结论;
(2)如图 2,当α=30°时,试判断四边形 BC1DA 的形状,并说明理由;
(3)在(2)的情况下,求 ED 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有( )

A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△ADE中,AB=AC,∠BAC=120°,∠ADE=90°,∠DAE=60°,F为BC中点,连接BE、DF,G、H分别为BE,DF的中点,连接GH.
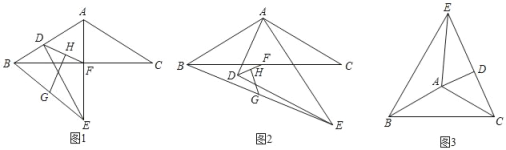
(1)如图1,若D在△ABC的边AB上时,请直接写出线段GH与HF的位置关系 ,![]() = .
= .
(2)如图2,将图1中的△ADE绕A点逆时针旋转至图2所示位置,其它条件不变,(1)中结论是否改变?请说明理由;
(3)如图3,将图1中的△ADE绕A点顺时针旋转至图3所示位置,若C、D、E三点共线,且AE=2,AC=![]() ,请直接写出线段BE的长 .
,请直接写出线段BE的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求证:无论m为任何实数,此函数图象与x轴总有两个交点;
(2)若此函数图象与x轴的一个交点为(-3,0),求此函数图象与x轴的另一个交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com