
����Ŀ�������ⱳ������ͼ1��ʾ����![]() �У�
��![]() ��
��![]() ����DΪֱ��
����DΪֱ��![]() �ϵĸ����㣨����B��C�غϣ�������
�ϵĸ����㣨����B��C�غϣ�������![]() �����߶�
�����߶�![]() �Ƶ�D��˳ʱ�뷽����ת90����ʹ��A��ת����E������
�Ƶ�D��˳ʱ�뷽����ת90����ʹ��A��ת����E������![]() .
.
�������̽�������D���߶�![]() ���˶���ͨ���۲졢������С���γ������µĽ���˼·������E��
���˶���ͨ���۲졢������С���γ������µĽ���˼·������E��![]() ��ֱ��
��ֱ��![]() ��F����ͼ2��ʾ��ͨ��֤��
��F����ͼ2��ʾ��ͨ��֤��![]() ______������֤
______������֤![]() ��_____�����Σ��Ӷ����
��_____�����Σ��Ӷ����![]() ______��.
______��.
������̽���������D���߶�![]() ���ӳ������˶�����ͼ3��ʾ�����
���ӳ������˶�����ͼ3��ʾ�����![]() �Ķ���.
�Ķ���.
����չ���죩����![]() ������D��ֱ��
������D��ֱ��![]() ���˶�ʱ����
���˶�ʱ����![]() ����ֱ��д��
����ֱ��д��![]() ����Сֵ.
����Сֵ.
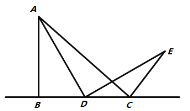
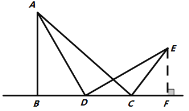
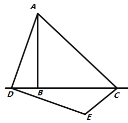
ͼ1 ͼ2 ͼ3
���𰸡���1����ADB������ֱ�ǣ�135�㣻��2��45�㣻��3��![]() .
.
��������
��1�������̽������ת�����ʵõ���ADE=90�㣬AD=DE�����ADB+��EDF=��ADB+��DAB=90�㣬�õ���DAB=��EDF�������AAS�õ���DEF�ա�ADB����EF=BD��DF=AB����AB=AC=DF���õ�BD=CF=EF�����CEF�ǵ���ֱ�������Σ��Ӷ��õ���DCE=135�㣻
��2������̽��������E��EG��CD���루1��ͬ������֤��ABD�ա�DGE���õ�BD=GE��AB=DG=BC����BD=CG=GE�����ɵõ�![]() ��
��
��3����չ���죺����D��ֱ��BC���˶�ʱ����BE��CEʱ��BE�ij�������Сֵ���ɣ�2����֪![]() �����BCEΪ����ֱ�������Σ���
�����BCEΪ����ֱ�������Σ���![]() .
.
�⣺��1�������̽����ͼ��
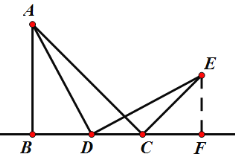
����ת�����ʣ��ã���ADE=90�㣬AD=DE��
���ADB+��EDF=90�㣬
�ߡ�ABC=90�㣬
���ADB+��DAB=90�㣬
���DAB=��EDF��
��EF��BC��
���ABC=��DFE=90�㣬
���ADB�ա�DEF��AAS����
��BD=EF��AB=DF��
��AB=DF=BC��
��BD+DC=DC+CF��
��BD=CF=EF��
���CEF�ǵ���ֱ�������Σ�
���CEF=45�㣬
���DCE=��CEF+��CFE=45��+90��=135�㣻
�ʴ�Ϊ����ADB������ֱ�ǣ�135�㣻
��2������̽������ͼ������E��EG��CD��
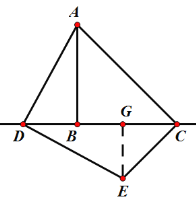
�ߡ�ADE=��ADB+��GDE=90�㣬��ADB+��DAB=90�㣬
���GDE=��DAB��
�ߡ�ABD=��DGE=90�㣬AD=DE��
���ABD�ա�DGE��AAS����
��BD=GE��AB=DG=BC��
��BD+BG=BG+GC��
��CG=BD=GE��
���CEG�ǵ���ֱ�������Σ�
���DCE=45�㣻
��3����չ���죺��ͼ������D��ֱ��BC���˶�ʱ����BE��CEʱ��BE�ij�������Сֵ��
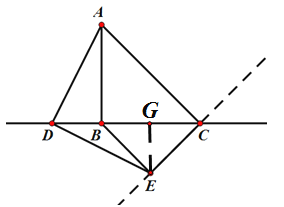
���BEC=90��.
�ɣ�2����֪����DCE=45�㣬
���BCE�ǵ���ֱ�������Σ�
��BE=CE��
��![]() ��
��
��![]() ��
��
��BE����СֵΪ![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() ���˶���
���˶���![]() ����״��Сʼ�ձ��ֲ��䣮���˶��Ĺ����У���
����״��Сʼ�ձ��ֲ��䣮���˶��Ĺ����У���![]() ����
����![]() ��������Ϊ______��
��������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
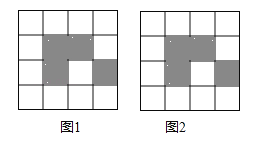
����Ŀ����ͼ������4��4����ͼ������16����ͬС��������ɣ�ÿ������ͼ����4��С��������Ϳ����Ӱ�����ڿհ�С�������У�������Ҫ��Ϳ����Ӱ��
��1����ͼ1��ѡȡ2���հ�С������Ϳ����Ӱ��ʹ6����ӰС���������һ�����ĶԳ�ͼ�Σ�
��2����ͼ2��ѡȡ2���հ�С������Ϳ����Ӱ��ʹ6����ӰС���������һ����Գ�ͼ�Σ����������ĶԳ�ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE.
��1����֤��CE��AD��
��2����DΪAB�е�ʱ���ı���BECD��ʲô�����ı��Σ�˵��������ɣ�
��3����DΪAB�е㣬��A�Ĵ�С����ʲô����ʱ���ı���BECD�������Σ���˵��������ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
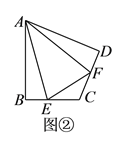
����Ŀ����![]() ����ͼ�٣����ı���
����ͼ�٣����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ��
��
��֤��![]() ��
��
��![]() ����ͼ�ڣ����ı���
����ͼ�ڣ����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �ϵĵ㣬��
�ϵĵ㣬��![]() ����
����![]() ���еĽ����Ƿ���Ȼ������
���еĽ����Ƿ���Ȼ������
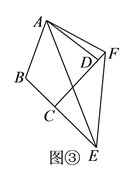
��![]() ����ͼ�ۣ����ı���
����ͼ�ۣ����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �ӳ����ϵĵ㣬��
�ӳ����ϵĵ㣬��![]() ����
����![]() ���еĽ����Ƿ���Ȼ����������������֤����������������д������֮���������ϵ����֤����
���еĽ����Ƿ���Ȼ����������������֤����������������д������֮���������ϵ����֤����
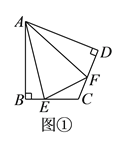
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ACƽ�֡�DAB��CE��AB��E��AB=AD+2BE�������н��ۣ���AB+AD=2AE���ڡ�DAB+��DCB=180������CD=CB����S��ACE��2S��BCE=S��ADC��������ȷ���۵ĸ����ǣ�������
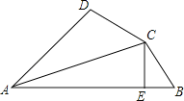
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У���֪
�У���֪![]() ��
��![]() ����
����![]() ��
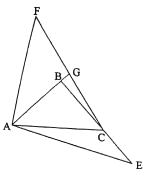
��![]() ���ӳ�����һ�㣬��ͼ��ʾ�����߶�
���ӳ�����һ�㣬��ͼ��ʾ�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() �� ��
�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���![]() ��ͼ�����н��۴�����ǣ� ��
��ͼ�����н��۴�����ǣ� ��
A.ͼ��һ������������
B.��![]() ��Ľ�������Ϊ
��Ľ�������Ϊ![]()
C.![]() ��
��![]() ���������С
���������С
D.ͼ�������������ཻ���γɵ�ֱ�������ε����Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵĺ�30���ǵ����dz߰���ͼ1��ʾ�ķ�ʽ�ڷ���һ�����ǽ϶̵�ֱ�DZ�BC��EC��3��
��1������ECD��ֱ��l����ƽ�Ƶ�ͼ2��λ�ã�ʹ��E������AB�ϣ���CC������ ����
��2������ECD�Ƶ�C��ʱ����ת��ͼ3��λ�ã�ʹ��E������AB�ϣ�����ECD�Ƶ�C��ת�Ķ���Ϊ�� ����
��3������ECD��ֱ��AC���۵�ͼ4��λ�ã�ED����AB�ཻ�ڵ�F����֤��AF��FD����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com