
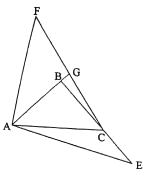
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是
是![]() 边延长线上一点,如图所示,将线段
边延长线上一点,如图所示,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() 交直线
交直线![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
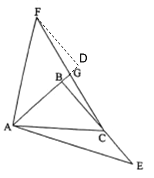
过点F作FD⊥AG,交AG的延长线于点D, 设BC=5x,利用AAS证出△FAD≌△AEB,从而用x表示出AD,BD,然后利用AAS证出△FDG≌△CBG,即可用x表示出BG,AG从而求出结论.
解:过点F作FD⊥AG,交AG的延长线于点D
∵![]()
设BC=5x,则CE=3x
∴BE=BC+CE=8x
∵![]() ,
,![]() ,
,
∴∠BAC=∠BCA=45°
∴∠BCA=∠CAE+∠E=45°
由旋转可知∠EAF=90°,AF=EA
∴∠CAE+∠FAD=∠EAF-∠BAC=45°
∴∠FAD=∠E
在△FAD和△AEB中
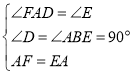
∴△FAD≌△AEB
∴AD=EB=8x,FD=AB
∴BD=AD-AB=3x,FD=CB
在△FDG和△CBG中
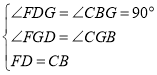
∴△FDG≌△CBG
∴DG=BG=![]() BD=
BD=![]()
∴AG=AB+BG=![]()
∴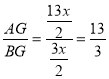
故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:
销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
若该店某天的销售价定为110元/件,雇有3名员工,则当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用):已知员工的工资为每人每天100元,每天还应支付其它费用为200元(不包括集资款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 | 芦柑 | 香梨 | |
每辆汽车载货量 | 7 | 6 | 5 |
每车水果获利 | 2500 | 3000 | 2000 |
![]() 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
![]() 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)如图1所示,在![]() 中,
中,![]() ,
,![]() ,点D为直线
,点D为直线![]() 上的个动点(不与B、C重合),连结
上的个动点(不与B、C重合),连结![]() ,将线段
,将线段![]() 绕点D按顺时针方向旋转90°,使点A旋转到点E,连结
绕点D按顺时针方向旋转90°,使点A旋转到点E,连结![]() .
.
(问题初探)如果点D在线段![]() 上运动,通过观察、交流,小明形成了以下的解题思路:过点E作
上运动,通过观察、交流,小明形成了以下的解题思路:过点E作![]() 交直线
交直线![]() 于F,如图2所示,通过证明
于F,如图2所示,通过证明![]() ______,可推证
______,可推证![]() 是_____三角形,从而求得
是_____三角形,从而求得![]() ______°.
______°.
(继续探究)如果点D在线段![]() 的延长线上运动,如图3所示,求出
的延长线上运动,如图3所示,求出![]() 的度数.
的度数.
(拓展延伸)连接![]() ,当点D在直线
,当点D在直线![]() 上运动时,若
上运动时,若![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
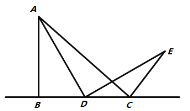
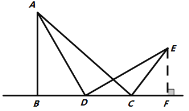
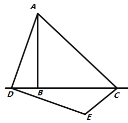
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为提升硬件设施,决定采购80台电脑,现有A,B两种型号的电脑可供选择.已知每台A型电脑比B型的贵2000元,2台A型电脑与3台B型电脑共需24000元.
(1)分别求A,B两种型号电脑的单价;
(2)若A,B两种型号电脑的采购总价不高于38万元,则A型电脑最多采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求平行四边形OABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=600,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
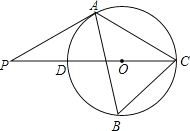
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=BC=2,∠ABC=120°,将△ABC 绕点 B 顺时针旋转角α(0°<α<90°)得△A1BC1,A1B 交 AC 于点 E,A1C1 分别交 AC、BC 于 D、F 两点.
(1)如图 1,观察并猜想,在旋转过程中,线段 EA1 与 FC 有怎样的数量关系? 并证明你的结论;
(2)如图 2,当α=30°时,试判断四边形 BC1DA 的形状,并说明理由;
(3)在(2)的情况下,求 ED 的长.
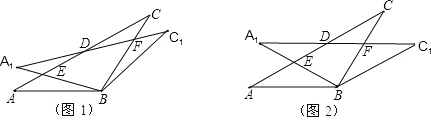
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com