
【题目】如图,△ABC内接于⊙O,∠B=600,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
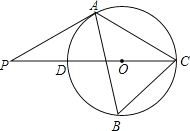
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
【答案】(1)见解析(2)2![]()
【解析】解:(1)证明:连接OA,
∵∠B=600,∴∠AOC=2∠B=1200。
∵OA=OC,∴∠OAC=∠OCA=300。
又∵AP=AC,∴∠P=∠ACP=300。
∴∠OAP=∠AOC﹣∠P=900。∴OA⊥PA。
∵OA是⊙O的半径,∴PA是⊙O的切线。
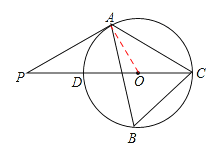
(2)在Rt△OAP中,∵∠P=300,
∴PO=2OA=OD+PD。
又∵OA=OD,∴PD=OA。
∵PD=![]() ,∴2OA=2PD=2
,∴2OA=2PD=2![]() 。
。
∴⊙O的直径为2![]() 。.
。.
(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=300,再由AP=AC得出
∠P=300,继而由∠OAP=∠AOC﹣∠P,可得出OA⊥PA,从而得出结论。
(2)利用含300的直角三角形的性质求出OP=2OA,可得出OP﹣PD=OD,再由PD=![]() ,可得出⊙O的直径。
,可得出⊙O的直径。


科目:初中数学 来源: 题型:
【题目】电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.
(1)求该品牌电动车销售量的月平均增长率;
(2)若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
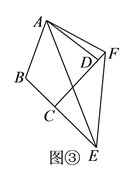
【题目】(![]() )如图①,在四边形
)如图①,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() .
.
求证:![]() .
.
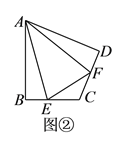
(![]() )如图②,在四边形
)如图②,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() ,(
,(![]() )中的结论是否仍然成立?
)中的结论是否仍然成立?
(![]() )如图③,在四边形
)如图③,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 延长线上的点,且
延长线上的点,且![]() .(
.(![]() )中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
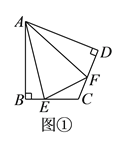
查看答案和解析>>
科目:初中数学 来源: 题型:
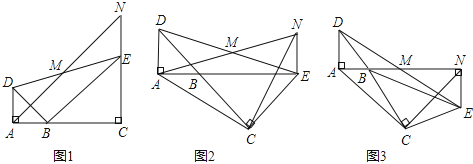
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数![]() 的图象,下列结论错误的是( )
的图象,下列结论错误的是( )
A.图象经过一、二、四象限
B.与![]() 轴的交点坐标为
轴的交点坐标为![]()
C.![]() 随
随![]() 的增大而减小
的增大而减小
D.图象与两坐标轴相交所形成的直角三角形的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让“两会”精神深入青年学生,增强学子们的历史使命和社会责任感,某高校党委举办了“奋力奔跑同心追梦”两会主题知识竞答活动,文学社团为选派优秀同学参加学校竞答活动,提前对甲、乙两位同学进行了6次测验:
①收集数据:分别记录甲、乙两位同学6次测验成绩(单位:分)
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
②整理数据:列表格整理两位同学的测验成绩(单位:分)
1 | 2 | 3 | 4 | 5 | 6 | |
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
③描述数据:根据甲、乙两位同学的成绩绘制折线统计图

④分析数据:两组成绩的平均数、中位数、众数、方差如下表:
同学 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 84 | 82.5 | __________ | 16.3 |
乙 | 84 | 83.5 | 83 | __________ |
得出结论:结合上述统计过程,回答下列问题:
(1)补全④中表格;
(2)甲、乙两名同学中,_______(填甲或乙)的成绩更稳定,理由是______________________
(3)如果由你来选择一名同学参加学校的竞答活动,你会选择__________(填甲或乙),理由是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴交于A(﹣2,0)、B(4,0)两点,且函数经过点(3,10).
(1)求二次函数的解析式;
(2)设这个二次函数的顶点为P,求△ABP的面积;
(3)当x为何值时,y≤0.(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机取出一个小球,记下数字为
,小红在剩下的3个小球中随机取出一个小球,记下数字为![]() 。
。
(1)计算由![]() 、
、![]() 确定的点
确定的点![]() 在函数
在函数![]() 的图象上的概率;
的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若![]() 、
、![]() 满足
满足![]() >6则小明胜,若
>6则小明胜,若![]() 、
、![]() 满足
满足![]() <6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
<6则小红胜,这个游戏公平吗?说明理由.若不公平,请写出公平的游戏规则.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com