
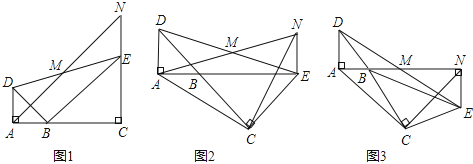
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)△ACN仍为等腰直角三角形,证明见解析.
【解析】
试题(1)由EN∥AD和点M为DE的中点可以证到△ADM≌△NEM,从而证到M为AN的中点.
(2)易证AB=DA=NE,∠ABC=∠NEC=135°,从而可以证到△ABC≌△NEC,进而可以证到AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形.
(3)同(2)中的解题可得AB=DA=NE,∠ABC=∠NEC=180°﹣∠CBN,从而可以证到△ABC≌△NEC,进而可以证到AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形.
试题解析:解:(1)证明:如图1,
∵EN∥AD,∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为DE的中点,∴DM=EM.
在△ADM和△NEM中,∵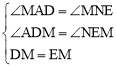 ,∴△ADM≌△NEM(AAS).
,∴△ADM≌△NEM(AAS).
∴AM=MN.∴M为AN的中点.
(2)证明:如图2,
∵△BAD和△BCE均为等腰直角三角形,∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD∥NE,∴∠DAE+∠NEA=180°.
∵∠DAE=90°,∴∠NEA=90°.∴∠NEC=135°.
∵A,B,E三点在同一直线上,∴∠ABC=180°﹣∠CBE=135°.∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),∴AD=NE.
∵AD=AB,∴AB=NE.
在△ABC和△NEC中,∵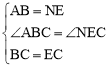 ,∴△ABC≌△NEC(SAS).
,∴△ABC≌△NEC(SAS).
∴AC=NC,∠ACB=∠NCE.∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
(3)△ACN仍为等腰直角三角形.证明如下:
如图3,此时A、B、N三点在同一条直线上.
∵AD∥EN,∠DAB=90°,∴∠ENA=∠DAN=90°.
∵∠BCE=90°,∴∠CBN+∠CEN=360°﹣90°﹣90°=180°.
∵A、B、N三点在同一条直线上,∴∠ABC+∠CBN=180°.∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),∴AD=NE.
∵AD=AB,∴AB=NE.
在△ABC和△NEC中,∵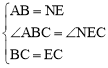 ,∴△ABC≌△NEC(SAS).
,∴△ABC≌△NEC(SAS).
∴AC=NC,∠ACB=∠NCE.∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
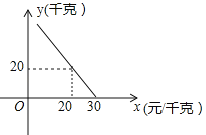
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为提升硬件设施,决定采购80台电脑,现有A,B两种型号的电脑可供选择.已知每台A型电脑比B型的贵2000元,2台A型电脑与3台B型电脑共需24000元.
(1)分别求A,B两种型号电脑的单价;
(2)若A,B两种型号电脑的采购总价不高于38万元,则A型电脑最多采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=600,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
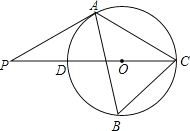
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放学后,小刚和同学边聊边往家走,突然想起今天是妈妈的生日,赶紧加快速度,跑步回家.小刚离家的距离![]() 和放学后的时间
和放学后的时间![]() 之间的关系如图所示,给出下列结论:①小刚家离学校的距离是
之间的关系如图所示,给出下列结论:①小刚家离学校的距离是![]() ;②小刚跑步阶段的速度为
;②小刚跑步阶段的速度为![]() ;③小刚回到家时已放学10分钟;④小刚从学校回到家的平均速度是
;③小刚回到家时已放学10分钟;④小刚从学校回到家的平均速度是![]() .其中正确的个数是( )
.其中正确的个数是( )
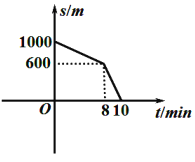
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=ax2+bx+c的图象过点(﹣1,0)和(m,0),请思考下列判断:①abc<0;②4a+c<2b;③![]() =1﹣
=1﹣![]() ;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=
;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=![]() 正确的是( )
正确的是( )
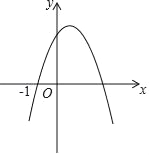
A. ①③⑤ B. ①②③④⑤ C. ①③④ D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三个不透明的布袋中分别放入一些除颜色不同外其他都相同的玻璃球,并搅匀,具体情况如下表:

在下列事件中,哪些是随机事件,哪些是必然事件,哪些是不可能事件?
(1) 随机从第一个布袋中摸出一个玻璃球,该球是黄色、绿色或红色的;
(2) 随机的从第二个布袋中摸出两个玻璃球,两个球中至少有一个不是绿色的;
(3) 随机的从第三个布袋中摸出一个玻璃球,该球是红色的;
(4)随机的从第一个布袋中和第二个布袋中各摸出一个玻璃球,两个球的颜色一致.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com