
【题目】一块含45°的直角三角板ABC, AB=AC, ∠BAC=90°, 点D为射线CB上一点,且不与点C,点B重合,连接AD.过点A作线段AD的垂线l,在直线l上,截取AE=AD(点E与点C在直线AD的同侧),连接CE.
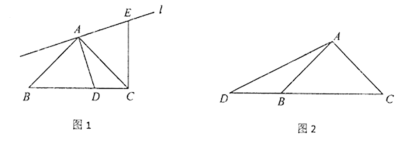
(1)当点D在线段CB上时,如图1,线段CE与BD的数量关系为____________,位置关系为___________;
(2)当点D在线段CB的延长线上时,如图2,
①请将图形补充完整;
②(1)中的结论是否仍成立?如果成立,请证明;如果不成立,请说明理由.
【答案】(1)CE=BD, CE⊥BD;(2)①见解析,②成立,理由见解析
【解析】
(1)在图1中证明△ABD≌△ACE,得到CE=BD,∠B=∠ACE=45°即可得到∠BCE=90°,即CE⊥BD;
(2)①根据题意,画出图形即可;
②与(1)同理,证明△ADB≌△AEC,然后得到CE=BD,然后得到∠ABC=∠ACB=45°,然后得到∠BCE=90°,即CE⊥BD.
证明:(1)∵AD⊥l,
∴∠DAE=∠BAC=90°,
∴∠BAD+∠DAC=∠DAC+∠CAE=90°,
∴∠BAD=∠CAE,
∵AD=AE,AB=AC,
∴△ABD≌△ACE,
∴CE=BD,∠B=∠ACE=45°,
∴∠ACB+∠ACE=45°+45°=90°,
∴∠BCE=90°,即CE⊥BD;
故答案为:CE=BD,CE⊥BD;
(2)①补全图形,如图:
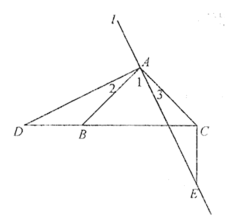
②CE=BD,CE⊥BD仍成立;
证明:∵AD⊥AE
∴∠DAE=90°
∵∠BAC=90°
∴∠DAE![]() ∠1=∠BAC
∠1=∠BAC![]() ∠1
∠1
即∠2=∠3
∵AB=AC, AD=AE
∴△ADB≌△AEC
∴CE=BD,∠ACE=∠ABD
∵∠ABC=∠ACB=45°
∴∠ACE=∠ABD=135°
∴∠DCE=∠ACE![]() ∠ACB=90°
∠ACB=90°
∴CE⊥BD.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 由
由![]() 绕点
绕点![]() 顺时针旋转得到,其中点
顺时针旋转得到,其中点![]() 与点
与点![]() 、点
、点![]() 与点
与点![]() 是对应点,连接
是对应点,连接![]() ,且
,且![]() 、
、![]() 、
、![]() 在同一条直线上,则
在同一条直线上,则![]() 的长为( )
的长为( )

A. 3 B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°,对角线AC,BD相交于点O,动点P从点A出发,以4cm/s的速度,沿A→B的路线向点B运动;过点P作PQ∥BD,与AC相交于点Q,设运动时间为t秒,0<t<5.

(1)设四边形PQCB的面积为S,求S与t的关系式;
(2)若点Q关于O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N,当t为何值时,点P、M、N在一直线上?
(3)直线PN与AC相交于H点,连接PM,NM,是否存在某一时刻t,使得直线PN平分四边形APMN的面积?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,5),B(12,0),在y轴负半轴上取点E,使OA=EO,作∠CEF=∠AEB,直线CO交BA的延长线于点D.

(1)根据题意,可求得OE= ;
(2)求证:△ADO≌△ECO;
(3)动点P从E出发沿E﹣O﹣B路线运动速度为每秒1个单位,到B点处停止运动;动点Q从B出发沿B﹣O﹣E运动速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间△OPM与△OQN全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的直角边
的直角边![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第象限,将
在第象限,将![]() 绕点
绕点![]() 按逆时针方向旋转至
按逆时针方向旋转至![]() ,使点
,使点![]() 的对应点
的对应点![]() 落在
落在![]() 轴的正半轴上,已知
轴的正半轴上,已知![]() ,
,![]() .
.

![]() 求点
求点![]() 和点
和点![]() 的坐标;
的坐标;
![]() 求经过点
求经过点![]() 和点
和点![]() 的直线所对应的一次函数解析式,并判断点
的直线所对应的一次函数解析式,并判断点![]() 是否在直线
是否在直线![]() 上.
上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组在楼![]() 的顶部
的顶部![]() 处测得该楼正前方旗杆
处测得该楼正前方旗杆![]() 的顶端
的顶端![]() 的俯角为
的俯角为![]() ,在楼
,在楼![]() 的底部
的底部![]() 处测得旗杆
处测得旗杆![]() 的顶端
的顶端![]() 的仰角为
的仰角为![]() ,已知旗杆
,已知旗杆![]() 的高度为
的高度为![]() ,根据测得的数据,计算楼
,根据测得的数据,计算楼![]() 的高度(结果保留整数).
的高度(结果保留整数).
参考数据:![]() ,
,![]() ,
,![]() .
.
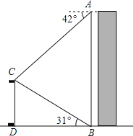
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=![]() x2﹣
x2﹣![]() x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D
x﹣3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D

(1)求出点A,B,D的坐标;
(2)如图1,若线段OB在x轴上移动,且点O,B移动后的对应点为O′,B′.首尾顺次连接点O′、B′、D、C构成四边形O′B′DC,请求出四边形O′B′DC的周长最小值.
(3)如图2,若点M是抛物线上一点,点N在y轴上,连接CM、MN.当△CMN是以MN为直角边的等腰直角三角形时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )

A. 19.2° B. 8° C. 6° D. 3°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com