
����Ŀ����ͼ������ABCD�ı߳�Ϊ20cm����ABC=120�����Խ���AC��BD�ཻ�ڵ�O������P�ӵ�A��������4cm/s���ٶȣ���A��B��·�����B�˶�������P��PQ��BD����AC�ཻ�ڵ�Q�����˶�ʱ��Ϊt�룬0��t��5��

��1�����ı���PQCB�����ΪS����S��t�Ĺ�ϵʽ��
��2������Q����O�ĶԳƵ�ΪM������P�Ҵ�ֱ��AB��ֱ��l������ABCD�ı�AD����CD���ڵ�N����tΪ��ֵʱ����P��M��N��һֱ���ϣ�
��3��ֱ��PN��AC�ཻ��H�㣬����PM��NM���Ƿ����ijһʱ��t��ʹ��ֱ��PNƽ���ı���APMN������������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1) S=��2![]() ��0��t��5���� (2)
��0��t��5���� (2) ![]() ;(3)������.
;(3)������.
��������
��1����ͼ1������S=S��ABC-S��APQ������ɵ�S��t�Ĺ�ϵʽ��
��2����PM=x����AM=2x���ɵ�AP=![]() x=4t������x��ֵ������ֱ��������30�Ƚǵ����ʿɵ�AM=2PM=
x=4t������x��ֵ������ֱ��������30�Ƚǵ����ʿɵ�AM=2PM=![]() ������AM=AO+OM���з��̿ɵ�t��ֵ��
������AM=AO+OM���з��̿ɵ�t��ֵ��
��3�����ڣ�ͨ����ͼ��֪��N��CD��ʱ��ֱ��PNƽ���ı���APMN����������������ȿɵ�MG=AP����AM=AO+OM����ʽ�ɵ�t��ֵ��
�⣺��1����ͼ1�����ı���ABCD�����Σ�
���ABD=��DBC=![]() ��ABC=60�㣬AC��BD��
��ABC=60�㣬AC��BD��
���OAB=30�㣬
��AB=20��
��OB=10��AO=10![]() ��
��
������ã�AP=4t��
��PQ=2t��AQ=2![]() t��
t��
��S=S��ABC��S��APQ��
=![]() ��
��
=![]() ��
��
=��2![]() t2+100
t2+100![]() ��0��t��5����
��0��t��5����
��2����ͼ2����Rt��APM�У�AP=4t��
�ߵ�Q����O�ĶԳƵ�ΪM��
��OM=OQ��
��PM=x����AM=2x��
��AP=![]() x=4t��
x=4t��
��x=![]() ��
��
��AM=2PM=![]() ��
��
��AM=AO+OM��
��![]() =10
=10![]() +10
+10![]() ��2
��2![]() t��
t��
t=![]() ��
��
�𣺵�tΪ![]() ��ʱ����P��M��N��һֱ���ϣ�
��ʱ����P��M��N��һֱ���ϣ�
��3�����ڣ�
��ͼ3����ֱ��PNƽ���ı���APMN�������
��S��APN=S��PMN��
��M��MG��PN��G��
�� ![]() ��
��
��MG=AP��
�á�APH�ա�MGH��
��AH=HM=![]() t��
t��
��AM=AO+OM��
ͬ����֪��OM=OQ=10![]() ��2
��2![]() t��
t��
![]() t=10
t=10![]() =10
=10![]() ��2
��2![]() t��
t��
t=![]() ��
��
�𣺵�tΪ![]() ��ʱ��ʹ��ֱ��PNƽ���ı���APMN�������
��ʱ��ʹ��ֱ��PNƽ���ı���APMN�������


 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��![]() ��
��![]() �IJ�����Ӧֵ���±���
�IJ�����Ӧֵ���±���
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�ҷ���![]() �������ֱ�Ϊ
�������ֱ�Ϊ![]() ��
��![]()
![]() ������˵��������ǣ� ����
������˵��������ǣ� ����
A. ![]() ��
��![]() B.
B. ![]()
C. ��![]() ʱ��
ʱ��![]() D. ��
D. ��![]() ʱ��
ʱ��![]() ����Сֵ
����Сֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ���ڸ�����˳�ν�ȡ
���ڸ�����˳�ν�ȡ![]() �������
�������![]() ��________�����Ϊ________��
��________�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�AC��BC����ACB��90������D��E�ֱ���AC��BC�ϣ���CD��CE��

��1����ͼ1����֤����CAE����CBD��
��2����ͼ2��F��BD���е㣬��֤��AE��CF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ��ӳ���ABCD�ı�CD,AB��E,F,ʹDE=BF,����EF,�ֱ�AD,BC��G,H������CG,AH.
��֤��CG��AH.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC������Ϊ��F�����������ĸ����ۣ��١�AEF�ס�CAB����CF=2AF����S��AEF��S��CAB=1��4����AF2=2EF2��������ȷ�Ľ����У�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����PΪ��ABC����ƽ����һ�㣬����APB=��BPC=��CPA=120�㣬���P������ABC�ķ����㣮
��1�������PΪ�����ABC�ķ����㣬����ABC=60�㣮
����֤����ABP�ס�BCP��
����PA=3��PC=4����PB= ��
��2����֪�����ABC���ֱ���AB��ACΪ������������ABE������ACD��CE��BD �ཻ��P�㣮��ͼ��2��
������CPD�Ķ�����
����֤��P��Ϊ��ABC�ķ����㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�麬45����ֱ�����ǰ�ABC, AB=AC, ��BAC=90���� ��DΪ����CB��һ�㣬�Ҳ����C,��B�غ�,����AD.����A���߶�AD�Ĵ���l,��ֱ��l�ϣ���ȡAE=AD(��E���C��ֱ��AD��ͬ��)������CE.
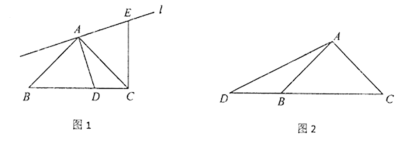
��1������D���߶�CB��ʱ����ͼ1,�߶�CE��BD��������ϵΪ____________��λ�ù�ϵΪ___________��
��2������D���߶�CB���ӳ�����ʱ����ͼ2,
���뽫ͼ�β�������;
�ڣ�1���еĽ����Ƿ��Գ���?�����������֤��;�������������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ס���������A�dz���������ʻ��B�ǣ���������ʻ�����У��ס��������뿪A�ǵľ���y��ǧ�ף���׳���ʻ��ʱ��t��ʱ��֮��Ĺ�ϵ��ͼ��ʾ���۲�ͼ��ش��������⣺
��1��A��B��������� ��ǧ��
��2��������ͬʱ�������ҳ����ȼ׳��絽�� ��Сʱ��
��3���ҳ��ĺ�����ϵʽΪ�� ����
��4���׳������� ����ʱ����������
��5�����ҳ���ʻ������/�������� ��Сʱ���ס����������40ǧ�ף�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com