
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△AEF:S△CAB=1:4;④AF2=2EF2.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
①根据四边形ABCD是矩形,BE⊥AC,可得∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故①正确;
②根据点E是AD边的中点,以及AD∥BC,得出△AEF∽△CBF,根据相似三角形对应边成比例,可得CF=2AF,故②正确;
③根据△AEF∽△CBF得到EF与BF的比值,据此求出S△AEF=![]() S△ABF,S△AEF=
S△ABF,S△AEF=![]() S△BCF,可得S△AEF:S△CAB=1:6,故③错误;
S△BCF,可得S△AEF:S△CAB=1:6,故③错误;
④根据AA可得△AEF∽△BAF,根据相似三角形的性质可得AF2=2EF2,故④正确.
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,
∴∠EAC=∠ACB,
∵BE⊥AC,
∴∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() =
=![]() ,
,
∵AE=![]() AD=
AD=![]() BC,
BC,
∴![]() =
=![]() ,
,
∴CF=2AF,故②正确;
∵△AEF∽△CBF,
∴EF:BF=1:2,
∴S△AEF=![]() S△ABF,S△AEF=
S△ABF,S△AEF=![]() S△BCF,
S△BCF,
∴S△AEF:S△CAB=1:6,故③错误;
∵△AEF∽△CAB,
∴∠AEF=∠BAF,
∵∠AFE=∠BFA=90°,
∴△AEF∽△BAF,
∴![]() ,
,
AF2=EFBF=2EF2,故④正确.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() 沿
沿![]() 轴向右平移后得到
轴向右平移后得到![]() ,点
,点![]() 的对应点
的对应点![]() 是直线
是直线![]() 上一点,则点
上一点,则点![]() 与其对应点
与其对应点![]() 间的距离为__________.
间的距离为__________.

B.比较![]() __________
__________![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实党中央“长江大保护”新发展理念,我市持续推进长江岸线保护,还洞庭湖和长江水清岸绿的自然生态原貌.某工程队负责对一面积为33000平方米的非法砂石码头进行拆除,回填土方和复绿施工,为了缩短工期,该工程队增加了人力和设备,实际工作效率比原计划每天提高了20%,结果提前11天完成任务,求实际平均每天施工多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°,对角线AC,BD相交于点O,动点P从点A出发,以4cm/s的速度,沿A→B的路线向点B运动;过点P作PQ∥BD,与AC相交于点Q,设运动时间为t秒,0<t<5.

(1)设四边形PQCB的面积为S,求S与t的关系式;
(2)若点Q关于O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N,当t为何值时,点P、M、N在一直线上?
(3)直线PN与AC相交于H点,连接PM,NM,是否存在某一时刻t,使得直线PN平分四边形APMN的面积?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了发展乡村旅游,某村准备在河道上修一座与河道垂直的桥,如图(1)所示,直线l,m代表河流的两岸河道,且l∥m,点A是某村自助农场的所在地,点B是某村游乐场所在地.

问题1:造桥选址桥准备选在到A,B两地的距离之和刚好为最小的点C处,即在直线l上找一点C,使AC+BC的值为最小.请利用你所学的知识在图(1)中作出点C的位置,并简单说明你所设计方案的原理;
问题2:测量河宽:在测量河道的宽度时施工队在河道南侧的开阔地用以下方法(如图2所示):①作CD⊥l,与河对岸的直线m相交于D;②在直线m上取E,F两点,使得DE=EF=10米;③过点F作m的垂线FG,使得点G与C,E两点在同一直线上;④测量FG的长度为20米.请你确定河道的宽度,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,5),B(12,0),在y轴负半轴上取点E,使OA=EO,作∠CEF=∠AEB,直线CO交BA的延长线于点D.

(1)根据题意,可求得OE= ;
(2)求证:△ADO≌△ECO;
(3)动点P从E出发沿E﹣O﹣B路线运动速度为每秒1个单位,到B点处停止运动;动点Q从B出发沿B﹣O﹣E运动速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间△OPM与△OQN全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
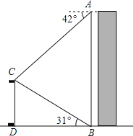
【题目】如图,某校数学兴趣小组在楼![]() 的顶部
的顶部![]() 处测得该楼正前方旗杆
处测得该楼正前方旗杆![]() 的顶端
的顶端![]() 的俯角为
的俯角为![]() ,在楼
,在楼![]() 的底部
的底部![]() 处测得旗杆
处测得旗杆![]() 的顶端
的顶端![]() 的仰角为
的仰角为![]() ,已知旗杆
,已知旗杆![]() 的高度为
的高度为![]() ,根据测得的数据,计算楼
,根据测得的数据,计算楼![]() 的高度(结果保留整数).
的高度(结果保留整数).
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
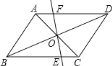
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于
相交于![]() 点,将直线
点,将直线![]() 绕点
绕点![]() 顺时针旋转,分别交
顺时针旋转,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 当旋转角为![]() 时,四边形
时,四边形![]() 一定为平行四边形
一定为平行四边形
B. 在旋转的过程中,线段![]() 与
与![]() 总相等
总相等
C. 当旋转角为![]() 时,四边形
时,四边形![]() 一定为菱形
一定为菱形
D. 当旋转角为![]() 时,四边形
时,四边形![]() 一定为等腰梯形
一定为等腰梯形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com