
 如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,DB垂直于x轴,CD=CB,M,N分别是线段BD,BC上的点,且∠CMN=∠DBC,
如图,在平面直角坐标系中,抛物线y=-$\frac{2}{3}$x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,DB垂直于x轴,CD=CB,M,N分别是线段BD,BC上的点,且∠CMN=∠DBC,分析 (1)利用待定系数法即可解决问题.
(2)根据两角对应相等的两个三角形相似即可判断.
(3)分三种情形讨论即可.
(4)设BM=x,BN=y则DM=4-x,由△CDM∽△MBN,得$\frac{CD}{BM}$=$\frac{DM}{BN}$,即$\frac{\sqrt{13}}{x}$=$\frac{4-x}{y}$,整理得x2-4x+$\sqrt{13}$y=0,根据方程有解,由△≥0,求出BN的最大值即可解决问题.
解答 解:(1)将点A、B的坐标代入抛物线的解析式得:$\left\{\begin{array}{l}{-\frac{2}{3}-b+c=0}\\{-6+3b+c=0}\end{array}\right.$,
解得:b=$\frac{4}{3}$,c=2.
所以抛物线的解析式为y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2.
(2)∵CD=CB,
∴∠D=∠BBM.
又∵∠CMN=∠DBC,
∴∠CMN=∠D.
∵∠DCM+∠D=∠CMN+∠NMB,
∴∠DCM=∠NMB.
∴△CDM∽△MBN.
(3)①NM=CN时,∵∠NCM=∠CMN=∠CBD=∠D,∠CBM=∠CBD,
∴△CBM∽△DBC,
∴$\frac{BC}{DB}$=$\frac{BM}{BC}$,
∴BM=$\frac{B{C}^{2}}{DB}$,
∵CD=BC,BD⊥AB,
∴D(3,4),
∴BC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,BD=4,
∴BM=$\frac{13}{4}$.
②MC=MN时,∵△CDM∽△MBN,
∴△CDM≌△△MBN,
∴BM=CD=$\sqrt{13}$.
③∵∠CNM=∠CBM+∠BMN>∠CMN,
∴CM>CN,
综上所述,当△CMN为等腰三角形时,BM的长为$\frac{13}{4}$或$\sqrt{13}$.
(4)设BM=x,BN=y则DM=4-x,
∵△CDM∽△MBN,
∴$\frac{CD}{BM}$=$\frac{DM}{BN}$,
∴$\frac{\sqrt{13}}{x}$=$\frac{4-x}{y}$,
整理得x2-4x+$\sqrt{13}$y=0,
∵方程有解,
∴△≥0,
∴16-4$\sqrt{13}$y≥0,
∴y≤$\frac{4\sqrt{13}}{13}$,
∴BN的最大值为$\frac{4\sqrt{13}}{13}$,
∵点M从D运动到B的过程中,N点由0到达最大值,再由最大值到达0,
∴点N运动的路径长为2×$\frac{4\sqrt{13}}{13}$=$\frac{8\sqrt{13}}{13}$.
点评 本题考查二次函数综合题、相似三角形的判定和性质、等腰三角形的判定和性质、一元二次方程,根的判别式等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,第四个问题的难点是BN的最大值的确定,属于中考压轴题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
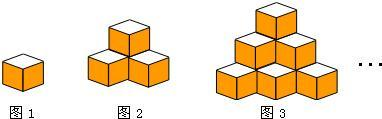
| n | 1 | 2 | 3 | 4 | … |
| S | 1 | 3 | 6 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
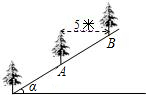 如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
如图.在坡角为a的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )| A. | 5cosa | B. | $\frac{5}{cosa}$ | C. | 5sina | D. | $\frac{5}{sina}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com