
【题目】如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
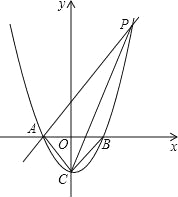
(1)求A、B、C三点的坐标;
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积;
(3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似?若存在,请求出M点的坐标;否则,请说明理由.
【答案】(1)A(-1,0),B(1,0),C(0,-1);(2)4;(3)M点的坐标为(-2,3),(![]() ,
,![]() ),(4,15).
),(4,15).
【解析】
试题分析:(1)抛物线与x轴的交点,即当y=0,C点坐标即当x=0,分别令y以及x为0求出A,B,C坐标的值;
(2)四边形ACBP的面积=△ABC+△ABP,由A,B,C三点的坐标,可知△ABC是直角三角形,且AC=BC,则可求出△ABC的面积,根据已知可求出P点坐标,可知点P到直线AB的距离,从而求出△ABP的面积,则就求出四边形ACBP的面积;
(3)假设存在这样的点M,两个三角形相似,根据题意以及上两题可知,∠PAC和∠MGA是直角,只需证明![]() 或
或![]() 即可.设M点坐标,根据题中所给条件可求出线段AG,CA,MG,CA的长度,然后列等式,分情况讨论,求解.
即可.设M点坐标,根据题中所给条件可求出线段AG,CA,MG,CA的长度,然后列等式,分情况讨论,求解.
试题解析:(1)令y=0,
得x2-1=0
解得x=±1,
令x=0,得y=-1
∴A(-1,0),B(1,0),C(0,-1);
(2)∵OA=OB=OC=1,
∴∠BAC=∠ACO=∠BCO=∠CBO=45°.
∵AP∥CB,
∴∠PAB=∠CBO=45°.
过点P作PE⊥x轴于E,则△APE为等腰直角三角形,
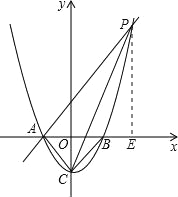
令OE=a,则PE=a+1,
∴P(a,a+1).
∵点P在抛物线y=x2-1上,
∴a+1=a2-1.
解得a1=2,a2=-1(不合题意,舍去).
∴PE=3.
∴四边形ACBP的面积S=![]() ABOC+
ABOC+![]() ABPE=
ABPE=![]() ×2×1+
×2×1+![]() ×2×3=4;
×2×3=4;
(3)假设存在
∵∠PAB=∠BAC=45°,
∴PA⊥AC
∵MG⊥x轴于点G,
∴∠MGA=∠PAC=90°
在Rt△AOC中,OA=OC=1,
∴AC=![]()
在Rt△PAE中,AE=PE=3,
∴AP=3![]()
设M点的横坐标为m,则M(m,m2-1)
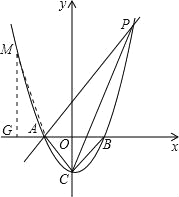
①点M在y轴左侧时,则m<-1.
(ⅰ)当△AMG∽△PCA时,有![]() .
.
∵AG=-m-1,MG=m2-1.
即![]()
解得m1=-1(舍去)m2=![]() (舍去).
(舍去).
(ⅱ)当△MAG∽△PCA时有![]() ,
,
即![]() .
.
解得:m=-1(舍去)m2=-2.
∴M(-2,3).
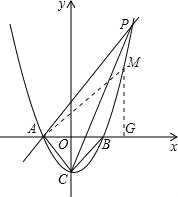
②点M在y轴右侧时,则m>1
(ⅰ)当△AMG∽△PCA时有![]()
∵AG=m+1,MG=m2-1
∴![]()
解得m1=-1(舍去)m2=![]() .
.
∴M(![]() ,
,![]() ).
).
(ⅱ)当△MAG∽△PCA时有![]() ,
,
即![]() .
.
解得:m1=-1(舍去)m2=4,
∴M(4,15).
∴存在点M,使以A、M、G三点为顶点的三角形与△PCA相似
M点的坐标为(-2,3),(![]() ,
,![]() ),(4,15).
),(4,15).


科目:初中数学 来源: 题型:
【题目】通过移项,将下列方程变形,错误的是( )
A. 由2x﹣3=﹣x﹣4,得2x﹣x=﹣4+3B. x+2=2x﹣7,得x-2x=﹣2-7
C. 5y﹣2=﹣6,得5y=﹣4D. 由x+3=2﹣4x,得5x=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沈阳地铁一号线的开通运行给沈阳市民的出行方式带来了一些变化.小王和小林准备利用课余时间,以问卷的方式对沈阳市民的出行方式进行调查.如图是沈阳地铁一号线图(部分),小王和小林分别从太原街站(用A表示)、南市场站(用B表示)、青年大街站(用C表示)这三站中,随机选取一站作为调查的站点.
⑴在这三站中,小王选取问卷调查的站点是太原街站的概率是多少?(请直接写出结果)
⑵请你用列表法或画树状图(树形图)法,求小王选取问卷调查的站点与小林选取问卷调查的站点相邻的概率.(各站点用相应的英文字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察、思考、解答: ( ![]() ﹣1)2=(
﹣1)2=( ![]() )2﹣2×1×
)2﹣2×1× ![]() +12=2﹣2
+12=2﹣2 ![]() +1=3﹣2
+1=3﹣2 ![]()
反之3﹣2 ![]() =2﹣2
=2﹣2 ![]() +1=(
+1=( ![]() ﹣1)2
﹣1)2
∴3﹣2 ![]() =(
=( ![]() ﹣1)2
﹣1)2
∴ ![]() =
= ![]() ﹣1
﹣1
(1)仿上例,化简: ![]() ;
;
(2)若 ![]() ,则m、n与a、b的关系是什么?并说明理由;
,则m、n与a、b的关系是什么?并说明理由;
(3)已知x= ![]() ,求(
,求( ![]() )
) ![]() 的值(结果保留根号)
的值(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,解答下列问题: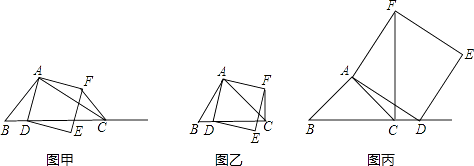
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系是什么?写出它们之间的数量关系.
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,请证明?
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?直接写出条件,不需要证明.
(3)若AC=4 ![]() ,BC=3,在(2)的条件下,求△ABC中AB边上的高.
,BC=3,在(2)的条件下,求△ABC中AB边上的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com