
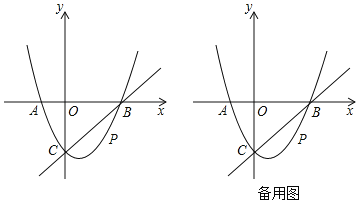
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��ax2��2x+c��ͼ����x�ύ��A��B���㣬��A��ԭ�����࣬��B������Ϊ��3��0������y�ύ�ڵ�C��0����3������P��ֱ��BC�·�����������һ���㣮
��1������κ����ı���ʽ��
��2������P�˶��������߶���ʱ�����ı���ABPC�������
��3����Q��x���ϵ�һ�����㣬����P���C���ڶԳ���Գ����Ե�B��C��P��QΪ������ı�����ƽ���ı���ʱ�����Q�����꣮
���𰸡���1��y��x2��2x��3����2��9����3��Q1��5��0����Q2��1��0����
��������
��1�����ô���ϵ������B��3��0����C��0��-3��������������y��ax2��2x+c���������ʽ���ɣ�
��2�����ı���ABPC�����������ָ�ΪS��AOC+S��OCP+S��OPB������������ε�������ɵó���
��3�����B��C��P��Q�������ٸ���ƽ���ı��ε����ʼ��ɽ��
�⣺��1����B��3��0����C��0����3��������������y��ax2��2x+c�ã�
![]() ��
��
���![]() ��
��
����κ����ı���ʽΪ��y��x2��2x��3��
��2����ͼ������P�˶��������߶���ʱ������AC��PC��PB��PO����PM��AB��PN��OC��
�߶��κ����ı���ʽΪy��x2��2x��3��
��P�������Ϊ��1����4������PN��1��PM��4�����ɵó�OB��3��OC��3��AO��1��
���ı���ABPC�������S��AOC+S��OCP+S��OPB
��![]() ��
��
��![]() ��
��
��9��
��3���ߵ�P���C���ڶԳ���Գƣ���C��0����3����
��P��2����3����PC��2��
�ߵ�Q��x���ϣ����Q��x��0����
��B��3��0����
��BQ��|x��3|��
���Ե�B��C��P��QΪ������ı�����ƽ���ı���ʱ��
��BQ��PC����BQ��PC��
��|x��3|��2��
��ã�x1��5��x2��1��
��Q1��5��0����Q2��1��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
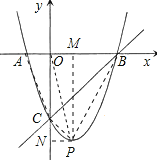
����Ŀ����ͼ1����![]() �У�
��![]() ����
����![]() �ֱ��DZ�
�ֱ��DZ�![]() ���е㣬����
���е㣬����![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת������ת��Ϊ
��ʱ�뷽����ת������ת��Ϊ![]() ��
��
![]() ���ⷢ��
���ⷢ��
![]() ��
��![]() ʱ��
ʱ��![]() �� ����
�� ����![]() ��
��![]() ʱ��
ʱ��![]() �� ����
�� ����
![]() ��չ̽��
��չ̽��
���жϣ���![]() ʱ��
ʱ��![]() �Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
�Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
![]() ������
������
![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת��
��ʱ����ת��![]() ������ͬһ��ֱ����ʱ�����߶�
������ͬһ��ֱ����ʱ�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019���й����������ղ�����(���¼����������)��4��29����10��7���ڱ������������У�����Ϊ�����ҵ������������������4��������ɫ��Ȥ��·�ߣ��ֱ��ǣ�![]() ����������������
����������������![]() �������Ҽң���������
�������Ҽң���������![]() ������С����֮������
������С����֮������![]() �������ٳ���֮�������������ŷ����ƻ����ȥ���ᣬ���Ǹ�������4����·������ѡ��һ����·������ÿ����·��ѡ��Ŀ�������ͬ��
�������ٳ���֮�������������ŷ����ƻ����ȥ���ᣬ���Ǹ�������4����·������ѡ��һ����·������ÿ����·��ѡ��Ŀ�������ͬ��
(1)����ѡ����·![]() ������С����֮�����ĸ����Ƕ��٣�
������С����֮�����ĸ����Ƕ��٣�
(2)�û���״ͼ���б��ķ��������������ŷ�ǡ��ѡ��ͬһ��·�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨѶ������Ѹ�ͷ�չ��������֮��Ĺ�ͨ��ʽ����������ݣ�ijУ��ѧ��ȤС������ˡ�����ϲ���Ĺ�ͨ��ʽ�������ʾ�(ÿ�˱�ѡ��ֻѡһ��)����ȫУ��Χ����������˲���ѧ������ͳ�ƽ������������������������ͳ��ͼ������ͼ����������Ϣ����������⣺
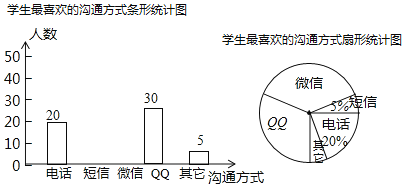
(1)���ͳ�ƹ�������� ����ѧ����������ͳ��ͼ�У���ʾ��QQ��������Բ�ĽǵĶ���Ϊ�� ����
(2)������ͳ��ͼ����������
(3)��У����1500��ѧ��������Ƹ�У��ϲ���á��š����й�ͨ��ѧ���ж�������
(4)ij��ס�������ͬѧ����ӡ��š�����QQ�������绰�����ֹ�ͨ��ʽ��ѡһ�ַ�ʽ��Է���ϵ�������б�����״ͼ�ķ�������ס�������ͬѧǡ��ѡ��ͬһ�ֹ�ͨ��ʽ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
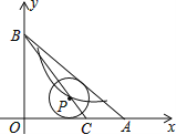
����Ŀ����ͼ����Rt��OAB�У�OA=4��AB=5����C��OA�ϣ�AC=1����P��Բ��P���߶�BC�ϣ��ҡ�P���AB��AO�����У�������������![]() ��k��0����ͼ��Բ��P����k=________________��
��k��0����ͼ��Բ��P����k=________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
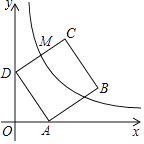
����Ŀ����ͼ��������ABCD�Ķ���A��D�ֱ���x�ᡢy���ϣ���ADO��30����OA��2����������y��![]() ����CD���е�M����ôk��_____��
����CD���е�M����ôk��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��һ����Ʒ������30Ԫ�������з���������Ʒÿ���������Ϧ��������ÿ�������ۼ�![]() ��Ԫ�������ϵ��
��Ԫ�������ϵ��![]() =100-2
=100-2![]() �����̵�ÿ������������ƷҪ���200Ԫ������������ôÿ����Ʒ���ۼ�Ӧ��Ϊ����Ԫ?ÿ��Ҫ�۳�������Ʒ���ټ�?
�����̵�ÿ������������ƷҪ���200Ԫ������������ôÿ����Ʒ���ۼ�Ӧ��Ϊ����Ԫ?ÿ��Ҫ�۳�������Ʒ���ټ�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y��![]() x��6��x�ᡢy��ֱ���B��C���㣬A����D��0��2��ΪԲ�ģ�2Ϊ�뾶��Բ��һ���㣬����AC��AB������ABC�������Сֵ�ǣ�������
x��6��x�ᡢy��ֱ���B��C���㣬A����D��0��2��ΪԲ�ģ�2Ϊ�뾶��Բ��һ���㣬����AC��AB������ABC�������Сֵ�ǣ�������
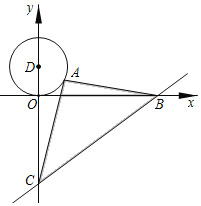
A. 26B. 24C. 22D. 20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��.ij�̳�Ϊ������ͣ����������,�⽨�����ͣ����,��ͼ�Ǹõ���ͣ�����µ���ڵ����ʾ��ͼ,����,AB��BD,��BAD=18��,C��BD��,BC=0.5 m.���ݹ涨,����ͣ�����µ�����Ϸ�Ҫ�����߱�־,�Ա��֪��ʻԱ���ݳ����ܷ�ȫʻ��.С����ΪCD�ij����������Ƶĸ߶�,��С����ΪӦ����CE�ij���Ϊ���Ƶĸ߶�.С����С��˭˵�ö�?�����жϲ��������ȷ�Ľ��.(�����ȷ��0.1 m,�ο�����:sin 18���0.31,cos 18���0.95,tan 18���0.325)
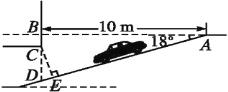
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com