
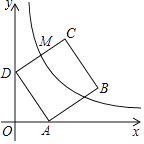
【题目】如图,正方形ABCD的顶点A、D分别在x轴、y轴上,∠ADO=30°,OA=2,反比例函y=![]() 经过CD的中点M,那么k=_____.
经过CD的中点M,那么k=_____.
【答案】![]() +6
+6
【解析】
先根据△CDE≌△DAO,得到DE=AO=2,DO=2![]() =CE,再根据F是CE的中点,即可得到F(
=CE,再根据F是CE的中点,即可得到F(![]() ,2+2
,2+2![]() ),最后根据反比例函数y=
),最后根据反比例函数y=![]() 的图象过CE的中点F,即可得到k的值.
的图象过CE的中点F,即可得到k的值.
解:如图,作CE⊥y轴于点E.
∵正方形ABCD的顶点A、D分别在x轴、y轴上,
∴∠CED=∠DOA=90°,∠DCE=∠ADO,CD=DA,
∴△CDE≌△DAO(AAS),
∴DE=AO=2,
又∵∠ODA=30°,
∴Rt△AOD中,AD=2AO=4,DO=2![]() =CE,
=CE,
∴EO=2+2![]() ,
,
∴C(2![]() ,2+2
,2+2![]() ),D(0,2
),D(0,2![]() ),
),
∵M是CD的中点,
∴M(![]() ,1+2
,1+2![]() ),
),
∵反比例函y=![]() 经过CD的中点M,
经过CD的中点M,
∴k=![]() (1+2
(1+2![]() )=
)=![]() +6,
+6,
故答案为:![]() +6.
+6.


科目:初中数学 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
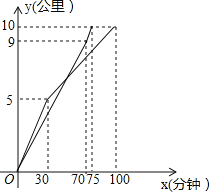
【题目】横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是![]() 公里/分;(2)乙在冲刺阶段的速度
公里/分;(2)乙在冲刺阶段的速度![]() 公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
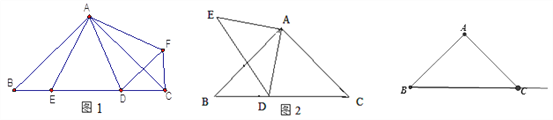
【题目】(1)如图1,在Rt△ABC 中, ![]() ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△![]() 绕点
绕点![]() 逆时针旋转90后,得到△
逆时针旋转90后,得到△![]() ,连接
,连接![]() .
.
(1)试说明:△![]() ≌△
≌△![]() ;
;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=ax2﹣2x+c的图象与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方的抛物线上一动点.
(1)求二次函数的表达式;
(2)当点P运动到抛物线顶点时,求四边形ABPC的面积;
(3)点Q是x轴上的一个动点,当点P与点C关于对称轴对称且以点B、C、P、Q为顶点的四边形是平行四边形时,求点Q的坐标.
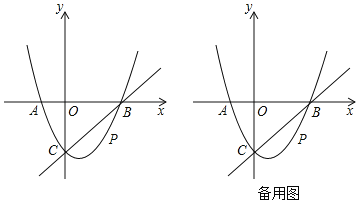
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A、B两种型号的污水处理设备共10台(注:要求同时有两种型号),买2台A型设备和3台B型设备共需要90万元,其中A型设备单价是B型设备单价的1.5倍;经预算,指挥部购买污水处理设备经费不超过180万元,请解答下列问题
(1)A型设备和B型设备的单价各是多少万元?
(2)指挥部有哪几种购买方案?
(3)若A型设备月处理污水量200吨、B型设各月处理污水量180吨,现要求月处理污水量不低于1840吨,设购买设备需要总费用为y万元,A型设备x台,请写出y与x的函数解析式,并根据函数性质选择更省钱的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
三等分任意角问题是数学史上一个著名的问题,直到1837年,数学家才证明了“三等分任意角”是不能用尺规完成的.
在探索中,出现了不同的解决问题的方法
方法一:
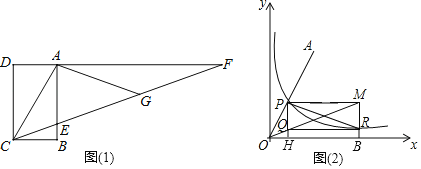
如图(1),四边形ABCD是矩形,F是DA延长线上一点,G是CF上一点,CF与AB交于点E,且∠ACG=∠AGC,∠GAF=∠F,此时∠ECB=![]() ∠ACB.
∠ACB.
方法二:
数学家帕普斯借助函数给出一种“三等分锐角”的方法(如图(2)):将给定的锐角∠AOB置于平面直角坐标系中,边OB在x轴上,边OA与函数y=![]() 的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=
的图象交于点P,以点P为圆心,以2OP长为半径作弧交图象于点R.过点P作x轴的平行线,过点R作y轴的平行线,两直线相交于点M,连接OM得到∠AOB,过点P作PH⊥x轴于点H,过点R作RQ⊥PH于点Q,则∠MOB=![]() ∠AOB.
∠AOB.
(1)在“方法一”中,若∠ACF=40°,GF=4,求BC的长.
(2)完成“方法二”的证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com