
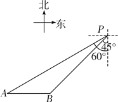
【题目】如图,一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)
【答案】(10![]() +10)海里
+10)海里
【解析】
利用题意得到AC⊥PC,∠APC=60°,∠BPC=45°,AB=20海里,如图,设BC=x海里,则AC=AB+BC=(20+x)海里.解△PBC,得出PC=BC=x海里,解Rt△APC,得出AC=PCtan60°=![]() x,根据AC不变列出方程
x,根据AC不变列出方程![]() x=20+x,解方程即可.
x=20+x,解方程即可.
如图,AC⊥PC,∠APC=60°,∠BPC=45°,AB=20海里,设BC=x海里,则AC=AB+BC=(20+x)海里.
在△PBC中,∵∠BPC=45°,
∴△PBC为等腰直角三角形,
∴PC=BC=x海里,
在Rt△APC中,∵tan∠APC=![]() ,
,
∴AC=PCtan60°=![]() x,
x,
∴![]() x=20+x,
x=20+x,
解得x=10![]() +10,
+10,
则PC=(10![]() +10)海里.
+10)海里.
答:轮船航行途中与灯塔P的最短距离是(10![]() +10)海里.
+10)海里.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
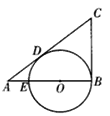
【题目】如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
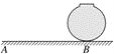
【题目】如图是置于水平地面上的一个球形储油罐,小敏想测量它的半径、在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的距离是10米(如示意图,AB=10米);同一时刻,他又测得竖直立在地面上长为1米的竹竿的影子长为2米,那么,球的半径是________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.

(1)求证:AD平分∠BAC;
(2)求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有何位置关系?(1) r=2cm;(2) r=2.4cm;(3) r=3cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
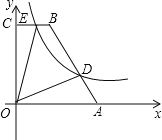
【题目】如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0), (2,6),点D为AB上一点,且BD=2AD,双曲线y=![]() (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
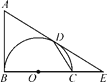
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com