
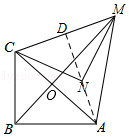
【题目】如图,在等腰直角三角形MNC中.CN=MN= ![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O. 
(1)∠NCO的度数为;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
【答案】
(1)15°
(2)证明:∵∠ACM=60°,CM=CA,
∴△CAM为等边三角形
(3)解:连接AN并延长,交CM于D,
∵△MNC是等腰直角三角形,△ACM是等边三角形,
∴NC=NM= ![]() ,CM=2,AC=AM=2,
,CM=2,AC=AM=2,
在△ACN和△AMN中,
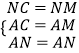 ,
,
∴△ACN≌△AMN(SSS),
∴∠CAN=∠MAN,
∴AD⊥CM,CD= ![]() CM=1,
CM=1,
∴Rt△ACD中,AD= ![]() CD=
CD= ![]() ,
,
等腰Rt△MNC中,DN= ![]() CM=1,
CM=1,
∴AN=AD﹣ND= ![]() ﹣1.
﹣1.
【解析】(1)由旋转可得∠ACM=60°,再根据等腰直角三角形MNC中,∠MCN=45°,运用角的和差关系进行计算即可得到∠NCO的度数;(2)根据有一个角是60°的等腰三角形是等边三角形进行证明即可;(3)根据△MNC是等腰直角三角形,△ACM是等边三角形,判定△ACN≌△AMN,再根据Rt△ACD中,AD= ![]() CD=
CD= ![]() ,等腰Rt△MNC中,DN=
,等腰Rt△MNC中,DN= ![]() CM=1,即可得到AN=AD﹣ND=
CM=1,即可得到AN=AD﹣ND= ![]() ﹣1.
﹣1.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对等边三角形的判定的理解,了解三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
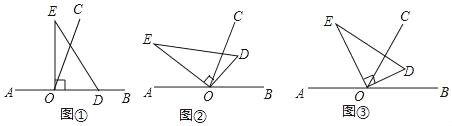
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
(1)S3= cm2(用含t的代数式表示);
(2)当点P运动几秒,S1=![]() S,说明理由;
S,说明理由;
(3)请你探索是否存在某一时刻,使得S1=S2=S3?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=36°,将△ABC绕点A按逆时针旋转角度ɑ(0°<ɑ<180°)得到△ADE,连接CE、BD,BD与CE相交于点F。
(1)求证:BD=CE
(2)当ɑ等于多少度时,四边形AFDE是平行四边形?并说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) 48![]() (
(![]() )- (-48)
)- (-48)![]() (-8) ;
(-8) ;
(2) 12 〡0.5![]() 〡
〡 ![]() 2 (3)2 ];
2 (3)2 ];
(3)先化简,再求值:
已知m 3, n ![]() ,求3m2n 2mn2 2(mn
,求3m2n 2mn2 2(mn ![]() m2n) mn] 3mn2 的值.
m2n) mn] 3mn2 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的课余生活,陶冶学生的情操,促进学生全面发展,某中学七年级开展了学生社团活动,学校为了解学生参加情况,对部分学生进行了调查,制作出如下的统计图:

请根据统计图,完成以下问题:
(1)这次共调查了 名学生;在扇形统计图中,表示“书法类”所在扇形的圆心角是 度.
(2)请把统计图1 补充完整.
(3)若七年级共有学生1100 名,请估算有多少名学生参加文学类社团.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘A、B中各个扇形的面积相等,且分别标有数字.小明和小丽玩转转盘游戏,规则如下:分别转动转盘A、B,当转盘停止转动时,将两个指针所指扇形内的数字相乘(若指针停在等分线上,那么重转一次). 
(1)用列表法(或树状图)分别求出数字之积为3的倍数及数字之积为5的倍数的概率;
(2)小亮和小丽想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得3分;数字之积为5的倍数时,小丽得4分,这个游戏对双方公平吗?请说明理由;认为不公平的,请你修改得分规定,使游戏双方公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com