
【题目】如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
(1)S3= cm2(用含t的代数式表示);
(2)当点P运动几秒,S1=![]() S,说明理由;
S,说明理由;
(3)请你探索是否存在某一时刻,使得S1=S2=S3?若存在,求出t值;若不存在,说明理由.

科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.
(1)直接写出计算结果:2③= ,(-3)④ = ,![]() ⑤= .
⑤= .
(2)计算 24÷23 + (-8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对八年级部分学生的数学成绩进行了质量监测(分数为整数,满分100分),根据质量监测成绩(最低分为53分)分别绘制了如下的统计表和统计图
分数 | 59.5分以下 | 59.5分以上 | 69.5分以上 | 79.5分以上 | 89.5分以上 |
人数 | 3 | 42 | 32 | 20 | 8 |
(1)求出被调查的学生人数,并补全频数直方图;
(2)若全市参加质量监测的学生大约有4500人,请估计成绩优秀的学生约有多少人?(80分及80分以上为优秀)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点C为线段AB上一点,AB=12,AC=8,点D为直线AB上一点,M、N分别是AB、CD的中点,若MN=10,则线段AD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
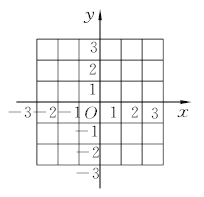
【题目】在平面直角坐标系中,点A关于y轴的对称点为点B,点B关于x轴的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出ΔABC,设AB与y轴的交点为D,求的值;
(2)若点A的坐标为(a,b)(ab≠0),判断ΔABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为m米,宽为n米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为40米,宽为25米,圆形花坛的半径为3米,求广场空地的面积(计算结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形MNC中.CN=MN= ![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O. 
(1)∠NCO的度数为;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com