
【题目】某市对八年级部分学生的数学成绩进行了质量监测(分数为整数,满分100分),根据质量监测成绩(最低分为53分)分别绘制了如下的统计表和统计图
分数 | 59.5分以下 | 59.5分以上 | 69.5分以上 | 79.5分以上 | 89.5分以上 |
人数 | 3 | 42 | 32 | 20 | 8 |
(1)求出被调查的学生人数,并补全频数直方图;
(2)若全市参加质量监测的学生大约有4500人,请估计成绩优秀的学生约有多少人?(80分及80分以上为优秀)

科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为-20,点B表示的数为16.动点P从点A出发,以每秒6个单位长度的速度沿数轴向右匀速运动,动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动.若点P、Q同时出发,设运动时间为t(t>0)秒.
(1)填空:①点A、B之间的距离为 ;
②点P表示的数为 ,点Q表示的数为 (用含t的代数式表示);
(2)当点P、Q到原点O的距离相等时,求t的值并求出此时点Q表示的数;
(3)若点P从点A出发到达点B后立刻返回到点A并保持速度不变,点Q到达点A时停止运动,问点P运动多少秒时与点Q相距6个单位长度?


查看答案和解析>>
科目:初中数学 来源: 题型:
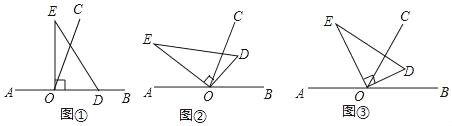
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
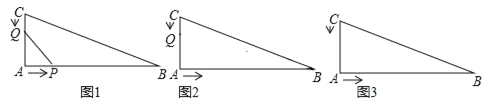
【题目】在直角三角形ABC中,若AB=16cm,AC=12cm,BC=20cm.点P从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,如果点P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,请用含t的代数式表示,①当点Q在AC上时,CQ= ;②当点Q在AB上时,AQ= ;
③当点P在AB上时,BP= ;④当点P在BC上时,BP= .
(2)如图2,若点P在线段AB上运动,点Q在线段CA上运动,当QA=AP时,试求出t的值.
(3)如图3,当P点到达C点时,P、Q两点都停止运动,当AQ=BP时,试求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+“是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(解决问题)
(1)求点A(-2.4),B(![]() +
+![]() -
-![]() )的勾股值[A],[B];
)的勾股值[A],[B];
(2)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
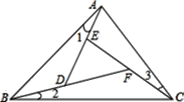
【题目】在学完三角形的内、外角后,教师要求同学们根据所学的知道设计一个利用“三角形一个外角等于与它不相邻的两个内角的和”求解的问题.如图:在△ABC中,∠1=∠2=∠3.
(1)试说明:∠BAC=∠DEF;
(2)若∠BAC=70°,∠DFE=50°,求∠ABC度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
(1)S3= cm2(用含t的代数式表示);
(2)当点P运动几秒,S1=![]() S,说明理由;
S,说明理由;
(3)请你探索是否存在某一时刻,使得S1=S2=S3?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com