
����Ŀ����ֱ��������ABC������AB=16cm��AC=12cm��BC=20cm����P�ӵ�A��ʼ��2����/����ٶ���A��B��C�ķ����ƶ�����Q�ӵ�C��ʼ��1����/����ٶ���C��A��B�ķ����ƶ��������P��Qͬʱ��������t���룩��ʾ�ƶ�ʱ������ô��
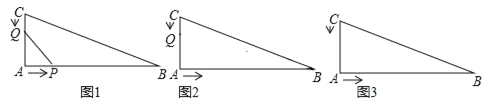
��1����ͼ1�����ú�t�Ĵ���ʽ��ʾ��������Q��AC��ʱ��CQ= ��������Q��AB��ʱ��AQ= ��
������P��AB��ʱ��BP= ��������P��BC��ʱ��BP= ��
��2����ͼ2������P���߶�AB���˶�����Q���߶�CA���˶�����QA=APʱ�������t��ֵ��
��3����ͼ3����P�㵽��C��ʱ��P��Q���㶼ֹͣ�˶�����AQ=BPʱ�������t��ֵ��
���𰸡���1��t��t��12��16��2t��2t��16����2��t=4����3��t=4��t=![]() ��
��
�������������������1�����������εı߳�������˶��ٶȽ��
��2�����������г����̣��ⷽ�̼��ɣ�
��3���ֵ�P���߶�AB���˶�����Q���߶�CA���˶�����P���߶�BC���˶�����Q���߶�CA���˶�����P���߶�BC���˶�����Q���߶�AB���˶���������г����̣��ⷽ�̼��ɣ�
�����������1���ٵ���Q��AC��ʱ��CQ=t��
�ڵ���Q��AB��ʱ��AQ=t-12��
�۵���P��AB��ʱ��BP=16-2t��
�ܵ���P��BC��ʱ��BP=2t-16��
�ʴ�Ϊ��t��t-12��16-2t��2t-16��
��2��������ã�12-t=2t��
��ã�t=4��
��3����AQ=BP
�൱��P���߶�AB���˶�����Q���߶�CA���˶�ʱ��12-t=16-2t��
��ã�t=4��
����P���߶�BC���˶�����Q���߶�CA���˶�ʱ��12-t=2t-16��
��ã�t=![]() ��
��
����P���߶�BC���˶�����Q���߶�AB���˶�ʱ��t-12=2t-16��
��ã�t=4���������⣩
��t=4��t=![]() ʱ��AQ=BP��
ʱ��AQ=BP��


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻС�����������ϵ�ij��![]() ����һ�δ�
����һ�δ�![]() ������1����λ��
������1����λ��![]() ���ڶ��δ�
���ڶ��δ�![]() ������2����λ��
������2����λ��![]() �������δ�
�������δ�![]() ������3����λ��
������3����λ��![]() �����Ĵδ�
�����Ĵδ�![]() ������4����λ��
������4����λ��![]() ����С���ԭ������������Ϲ�������6��ʱ�������������ϵĵ�
����С���ԭ������������Ϲ�������6��ʱ�������������ϵĵ�![]() ����ʾ������__________����С�����Ϲ�������2n��ʱ�������������ϵĵ�
����ʾ������__________����С�����Ϲ�������2n��ʱ�������������ϵĵ�![]() ����ʾ����ǡ����
����ʾ����ǡ����![]() ������ֻС��ij�ʼλ�õ�
������ֻС��ij�ʼλ�õ�![]() ����ʾ������__________.
����ʾ������__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��AC��AE��AF��BE��CF���ڵ�D����������н��ۣ��١�ABE�ա�ACF���ڡ�BDF�ա�CDE����D�ڡ�BAC��ƽ�����ϣ�������ȷ���ǣ�������
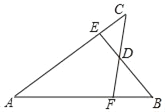
A. �� B. �� C. ������ D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������![]() ������������Щ������ʹ�������������磺a��b��0�����dz�ʹ��
������������Щ������ʹ�������������磺a��b��0�����dz�ʹ��![]() ������һ����a��bΪ��������ԡ�����Ϊ��a��b����
������һ����a��bΪ��������ԡ�����Ϊ��a��b����
(1)����1��b���ǡ�������ԡ�����b��ֵ��
(2)����m��n���ǡ�������ԡ�������m��0����![]() ��
��
(3)����m��n���ǡ�������ԡ��������ʽm��![]() ��[4m��2��3n��1��]��ֵ��
��[4m��2��3n��1��]��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��a��b��c��ʾ������·����Ҫ��һ��������תվ��Ҫ������������·�ľ�����ȣ���ɹ�ѡ��ĵ�ַ��_______��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ж��꼶����ѧ������ѧ�ɼ�������������⣨����Ϊ����������100�֣��������������ɼ�����ͷ�Ϊ53�֣��ֱ���������µ�ͳ�Ʊ���ͳ��ͼ
���� | 59.5������ | 59.5������ | 69.5������ | 79.5������ | 89.5������ |
���� | 3 | 42 | 32 | 20 | 8 |
��1������������ѧ������������ȫƵ��ֱ��ͼ��
��2����ȫ�вμ���������ѧ����Լ��4500�ˣ�����Ƴɼ������ѧ��Լ�ж����ˣ���80�ּ�80������Ϊ���㣩

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ı��ε�һ������������Ի�_____���Խ��ߣ����ı��ηֳ��� �������Σ��ı��ι���____���Խ��ߣ�
��2��������ε�һ������������Ի�_____���Խ��ߣ�������ηֳ��� �������Σ�����ι���____���Խ��ߣ�
��3���������ε�һ������������Ի�_____���Խ��ߣ��������ηֳ��� �������Σ������ι���____���Խ��ߣ�
��4�����룺�ٴ�100���ε�һ������������Ի�_____���Խ��ߣ���100���ηֳ��� �������Σ�100���ι���___���Խ��ߣ��ڴ�n���ε�һ������������Ի�_____���Խ��ߣ���n�ֳ��� �������Σ�n���ι���_____���Խ��ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
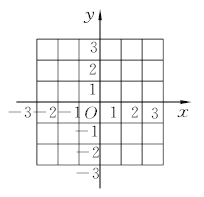
����Ŀ����ƽ��ֱ������ϵ��,��A����y��ĶԳƵ�Ϊ��B,��B����x��ĶԳƵ�Ϊ��C.
(1)����A������Ϊ(1,2),�����ڸ���������ϵ�л�����ABC,��AB��y��Ľ���ΪD,���ֵ;
(2)����A������Ϊ(a,b)(ab��0),�ж���ABC����״.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y=��2x+b��ͼ����x�ᡢy��ֱ���B��A���㣬�뷴��������y= ![]() ��x��0������C��D���㣮
��x��0������C��D���㣮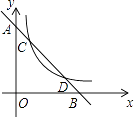
��1������D��������2��m������m= �� b=��
��2���ڣ�1���������£�ͨ�������ж�AC��BD��������ϵ��
��3������һ�κ���y=��2x+b�뷴��������y= ![]() ��x��0����ͼ���һ����ʼ�������������ǰ���£�����bΪ��ֵ����2����AC��BD��������ϵ�Ƿ���������˵�����ɣ�
��x��0����ͼ���һ����ʼ�������������ǰ���£�����bΪ��ֵ����2����AC��BD��������ϵ�Ƿ���������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com