
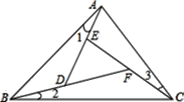
【题目】在学完三角形的内、外角后,教师要求同学们根据所学的知道设计一个利用“三角形一个外角等于与它不相邻的两个内角的和”求解的问题.如图:在△ABC中,∠1=∠2=∠3.
(1)试说明:∠BAC=∠DEF;
(2)若∠BAC=70°,∠DFE=50°,求∠ABC度数.
【答案】(1)证明见解析;(2)60°
【解析】
(1)根据三角形的一个外角等于与它不相邻的两个内角的和得出∠3+∠CAE=∠DEF,再根据∠1=∠3整理即可得证;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和得出∠2+∠BCF=∠DFE,再根据∠2=∠3即可得∠ACB=∠DFE,然后利用三角形的内角和等于180°求解即可.
(1)证明:在△ACE中,∠DEF=∠3+∠CAE,
∵∠1=∠3,
∴∠DEF=∠1+∠CAE=∠BAC,
即∠BAC=∠DEF;
(2)解:在△BCF中,∠DFE=∠2+∠BCF,
∵∠2=∠3,
∴∠DFE=∠3+∠BCF,
即∠DFE=∠ACB,
∵∠BAC=70°,∠DFE=50°,
∴在△ABC中,∠ABC=180°-∠BAC-∠ACB=180°-70°-50°=60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
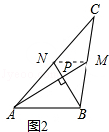
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)如图1,当tan∠PAB=1,c=4 ![]() 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)若(m,n)是“相伴数对”,其中m≠0,求![]() ;
;
(3)若(m,n)是“相伴数对”,求代数式m﹣![]() ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对八年级部分学生的数学成绩进行了质量监测(分数为整数,满分100分),根据质量监测成绩(最低分为53分)分别绘制了如下的统计表和统计图
分数 | 59.5分以下 | 59.5分以上 | 69.5分以上 | 79.5分以上 | 89.5分以上 |
人数 | 3 | 42 | 32 | 20 | 8 |
(1)求出被调查的学生人数,并补全频数直方图;
(2)若全市参加质量监测的学生大约有4500人,请估计成绩优秀的学生约有多少人?(80分及80分以上为优秀)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了 个三角形;四边形共有____条对角线.
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了 个三角形;五边形共有____条对角线.
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了 个三角形;六边形共有____条对角线.
(4)猜想:①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了 个三角形;100边形共有___条对角线.②从n边形的一个顶点出发可以画_____条对角线,把n分成了 个三角形;n边形共有_____条对角线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点C为线段AB上一点,AB=12,AC=8,点D为直线AB上一点,M、N分别是AB、CD的中点,若MN=10,则线段AD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
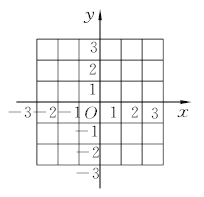
【题目】在平面直角坐标系中,点A关于y轴的对称点为点B,点B关于x轴的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出ΔABC,设AB与y轴的交点为D,求的值;
(2)若点A的坐标为(a,b)(ab≠0),判断ΔABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考
我们知道,在数轴上|a|表示数a所对应的点到原点的距离,这是绝对值的几何意义,由此我们可进一步地来研究数轴上任意两个点之间的距离,一般地,如果数轴上两点A、B 对立的数用a,b表示,那么这两个点之间的距离AB=|a﹣b|.也可以用两点中右边的点所表示数的减去左边的点所表示的数来计算,例如:数轴上P,Q两点表示的数分别是﹣1和2,那么P,Q两点之间的距离就是 PQ=2﹣(﹣1)=3.
启发应用
如图,点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0
(1)求线段AB的长;
(2)如图,点C在数轴上对应的数为x,且x是方程2x+1=![]() x﹣8的解,
x﹣8的解,
①求线段BC的长;
②在数轴上是否存在点P使PA+PB=BC?若存在,直接写出点P对应的数:若不存在,说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com