
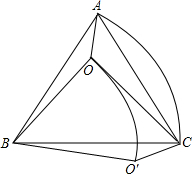
 ��ͼ��O�ǵȱߡ�ABC��һ�㣬OA=2��OB=3����AOB=150�㣬��BOC=115�㣬����AOB�Ƶ�B˳ʱ����ת60������CO��B������˵���У�
��ͼ��O�ǵȱߡ�ABC��һ�㣬OA=2��OB=3����AOB=150�㣬��BOC=115�㣬����AOB�Ƶ�B˳ʱ����ת60������CO��B������˵���У����� ������OO�䣬����ת�����ʿɵá�BOO���ǵȱ������Σ��á�OO��C=150��-60��=90�㣬�ɹ��ɶ����ɵ�OC�ij���
����S��ABO+SBOC=S��BO��C+S��BOC=S��BOO��+S��OO��C�����������ε������ʽ�ɵý����
���ɡ�OO��C=150��-60��=90�㣬��BOO��=60�㣬��BOC=115�㣬�á�O��OC�͡�OCO�䣻
�۹���A��AE��BO��BO���ӳ����ڵ�E����������Ǻ����ɵ�AE��OE����BE���ɹ��ɶ�����AB2���Ӷ��ó���ABC���������S��AOC-S��AOB=S��ABC-S��ABO-S��BOC-S��AOB�ý��ۣ�
�������������ABC������OBO���������ɵñ�AO��ɨ������������
��� �⣺������OO�䣬
�ߡ�ABC�ǵȱ������Σ�����AOB�Ƶ�B˳ʱ����ת60������CO��B��
���OBO��=60�㣬OB=O��B=3����AOB=��CO��B=150�㣬AO=CO��=2��
���BOO���ǵȱ������Σ�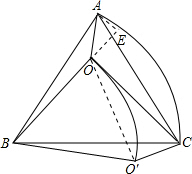
���OO��B=60�㣬OO��=BO=3��
���OO��C=150��-60��=90�㣬
�ɹ��ɶ����ã�OC=$\sqrt{{OO��}^{2}{+CO��}^{2}}$=$\sqrt{13}$��
�ʢ���ȷ��
��S��ABO+SBOC=S��BO��C+S��BOC=S��BOO��+S��OO��C
=$\frac{1}{2}��BO��BO���sin60��$+$\frac{1}{2}$��CO���OO��
=$\frac{1}{2}��3��3��\frac{\sqrt{3}}{2}$$+\frac{1}{2}��2��3$
=$\frac{9\sqrt{3}}{4}+3$��
�ʢ���ȷ��
����Rt��OO��C��
�ߡ�BOC=115�㣬��BOO��=60�㣬
���O��OC=115��-60��=55�㣬
���OCO��=180��-90��-55��=35�㣬
�ʢ���ȷ��
�۹���A��AE��BO��BO���ӳ����ڵ�E��
�ߡ�AOB=150�㣬
���AOE=30�㣬
��AE=1��OE=$\sqrt{3}$��
��AB2=BE2+AE2=${��3+\sqrt{3}��}^{2}{+1}^{2}$=13$+6\sqrt{3}$��
��S��ABC=$\frac{1}{2}$AB2•sin60��=$\frac{1}{2}����13+6\sqrt{3}����\frac{\sqrt{3}}{2}$=$\frac{13\sqrt{3}}{4}+\frac{9}{2}$��
S��AOC=S��ABC-��S��ABO+SBOC��=$\frac{13\sqrt{3}}{4}+\frac{9}{2}$-��$\frac{9\sqrt{3}}{4}+3$��=$\sqrt{3}+\frac{3}{2}$��
S��AOB=$\frac{1}{2}��AO��BO��sin30��$=$\frac{1}{2}��2��3��\frac{1}{2}$=$\frac{3}{2}$��
��S��AOC-S��AOB=$\sqrt{3}+\frac{3}{2}$-$\frac{3}{2}$=$\sqrt{3}$��
�ʢ۴���
�ݡ�S����ABC=$\frac{60��•��{•AB}^{2}}{360��}$=$\frac{��13+6\sqrt{3}����}{6}$��
S��AOB=S��CO��B=$\frac{3}{2}$��
S����OBO��=$\frac{60��•��{•BO}^{2}}{360��}$=$\frac{3��}{2}$��
���AO��ɨ�����������ǣ�S����ABC+S��BO��C-S��AOB-S����OBO��
=S����ABC-S����OBO��
=$\frac{13��}{6}$$+\sqrt{3}��$-$\frac{3��}{2}$
=$\frac{2��}{3}$$+\sqrt{3}��$��
�ʢݴ���
����ȷ������Т٢ڢܣ�
�ʴ�Ϊ���٢ڢܣ�
���� ������Ҫ���������ε������ʽ�������ε���������ɶ�����������ͼ�ε���������㣬���ν�ϣ���������ͼ�ε������Ϊ����ͼ�ε�����ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
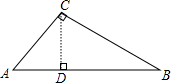 ��ͼ���ó�3m��4m��5m������ľ�����ô��һ��Rt��ABC��AC=3����C=90�㣬��һ����ֱ��AB��ƽ�й�������ȥ��AC��BC��AB��Ӱ���ֱ�ΪAD��DB����AD=$\frac{9}{5}$��BD=$\frac{16}{5}$��
��ͼ���ó�3m��4m��5m������ľ�����ô��һ��Rt��ABC��AC=3����C=90�㣬��һ����ֱ��AB��ƽ�й�������ȥ��AC��BC��AB��Ӱ���ֱ�ΪAD��DB����AD=$\frac{9}{5}$��BD=$\frac{16}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����COB=2��BOA���Խ���AC=10cm����AB�ij���
��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����COB=2��BOA���Խ���AC=10cm����AB�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x����ȫƽ���� | B�� | x-25����ȫƽ���� | ||
| C�� | x-50����ȫƽ���� | D�� | x+50����ȫƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��m��3 | B�� | 1��m��2��2��m��3 | C�� | m��1 | D�� | m��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
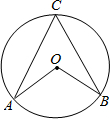 ��ͼ����ACB�͡�AOB�ǡ�0�л�AB���Ե�Բ�ܽǺ�Բ�Ľǣ���AOB=80�㣬��AB����Բ�ܽǵĶ����ǣ�������
��ͼ����ACB�͡�AOB�ǡ�0�л�AB���Ե�Բ�ܽǺ�Բ�Ľǣ���AOB=80�㣬��AB����Բ�ܽǵĶ����ǣ�������| A�� | 40�� | B�� | 45�� | C�� | 50�� | D�� | 80�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��С$\frac{1}{4}$ | B�� | ����4�� | C�� | û�б仯 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{{h}_{1}}{{h}_{2}}}$ | B�� | $\frac{\sqrt{{h}_{1}}}{\sqrt{{h}_{2}}}$ | C�� | $\frac{\sqrt{{h}_{1}{h}_{2}}}{{h}_{2}}$ | D�� | $\frac{\sqrt{{h}_{1}{h}_{2}}}{{h}_{1}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com