
| A. | 1<m<3 | B. | 1≤m<2或2<m<3 | C. | m<1 | D. | m>3 |
分析 函数y=(m-2)x2-4mx+2m-6的图象与x轴的负半轴至少有一个交点,分两种情况,一是有两个交点只有一个在负半轴,二是交点都在负半轴,分类解答即可.
解答 解:∵二次函数y=(m-2)x2-4mx+2m-6,
∴m-2≠0,
∴m≠2,
当①图象与x轴的交点有两个,原点的两侧各有一个,
则$\left\{\begin{array}{l}{△>0}\\{{x}_{1}{x}_{2}<0}\end{array}\right.$,
解得2<m<3;
②图象与x轴的交点都在x轴的负半轴,
则$\left\{\begin{array}{l}{△≥0}\\{{x}_{1}{x}_{2}=\frac{4m}{m-2}<0}\\{{x}_{1}{x}_{2}=\frac{2m-6}{m-2}>0}\end{array}\right.$,
解得:1≤m<2.
综上可得m的取值范围是:1≤m<2或2<m<3
故选B.
点评 本题考查一元二次方程根的分布与系数的关系以及抛物线和x轴交点的问题,是基础题,难度不大,但不要漏解,解题的关键是注意分类讨论思想的运用.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌/元 | +2.8 | +3 | -2 | +1.5 | -2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
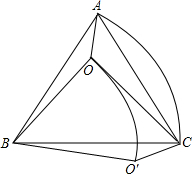 如图,O是等边△ABC中一点,OA=2,OB=3,∠AOB=150°,∠BOC=115°,将△AOB绕点B顺时针旋转60°至△CO′B,下列说法中:
如图,O是等边△ABC中一点,OA=2,OB=3,∠AOB=150°,∠BOC=115°,将△AOB绕点B顺时针旋转60°至△CO′B,下列说法中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
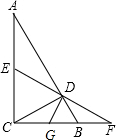 如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com