
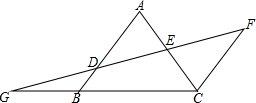
 如图,AB∥FC,D是AB上一点,且DE=EF,DF交AC于点E,分别延长FD和CB交于点G
如图,AB∥FC,D是AB上一点,且DE=EF,DF交AC于点E,分别延长FD和CB交于点G分析 (1)根据两角及其夹边分别对应相等的两个三角形全等,判断出△ADE≌△CFE即可.
(2)首先根据相似三角形判定的方法,判断出△GBD∽△GCF,推得$\frac{GB}{GC}$=$\frac{BD}{CF}$,据此求出CF的值是多少;然后根据△ADE≌△CFE,求出AD的值是多少,即可求出AB的长是多少.
解答 (1)证明:∵AB∥FC,
∴∠ADE=∠CFE,
在△ADE和△CFE中,
$\left\{\begin{array}{l}{∠ADE=∠CFE}\\{DE=EF}\\{∠AED=∠CEF}\end{array}\right.$
∴△ADE≌△CFE.
(2)解:∵AB∥FC,
∴△GBD∽△GCF,
∴$\frac{GB}{GC}$=$\frac{BD}{CF}$,
∴$\frac{2}{2+4}=\frac{1}{CF}$,
∴CF=3,
∵△ADE≌△CFE,
∴AD=CF=3,
∴AB=AD+BD=3+1=4.
点评 此题主要考查了相似三角形的判定与性质,以及全等三角形的判定与性质,要熟练掌握.


科目:初中数学 来源: 题型:解答题
 小华和爸爸上山游玩,爸爸乘电缆车,小华步行,两人相约在山顶的缆车终点会合.已知小华行走到缆车终点的路程是爸爸乘缆车到山顶的线路长的2倍,爸爸在小华出发后50min才乘上电缆车,电缆车的平均速度为180m/min.设小华出发x(min)行走的路程为y(m),图中的折线表示小华在整个行走过程中y(m)与x(min)之间的函数关系.
小华和爸爸上山游玩,爸爸乘电缆车,小华步行,两人相约在山顶的缆车终点会合.已知小华行走到缆车终点的路程是爸爸乘缆车到山顶的线路长的2倍,爸爸在小华出发后50min才乘上电缆车,电缆车的平均速度为180m/min.设小华出发x(min)行走的路程为y(m),图中的折线表示小华在整个行走过程中y(m)与x(min)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,路灯(P点)距地面9米,身高1.5米的小云从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
如图,路灯(P点)距地面9米,身高1.5米的小云从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com