
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����κ���y����
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����κ���y����![]() +bx+c��ͼ��B��C���㣬����x��ĸ����ύ�ڵ�A��
+bx+c��ͼ��B��C���㣬����x��ĸ����ύ�ڵ�A��
(1)����κ����ı���ʽ��
(2)��ͼ1����D�������ߵ��������ϵ�һ���㣬����DC��DB����S��DCB��S��ABCʱ�����D���ꣻ
(3)��ͼ2����(2)�������£���Q��CA���ӳ����ϣ�����DQ��AD������Q��QP��y�ᣬ����������P������AQD����ACO+��ADC�������PQ�ij���
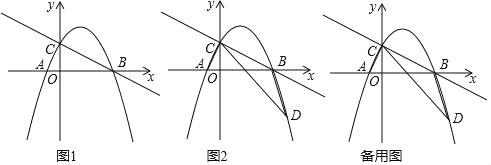
���𰸡���1��![]() ����2��
����2��![]() ����3��6
����3��6
��������
��1�������B��C�����꣬Ȼ�������κ����Ľ���ʽ���ⷽ���鼴�ɣ�
(2)��D��DG��x����G����C��CF��DG��F����B��BE��CF��E����D��x��y������x��0��y��0�����S��ABC������S��CBD=S��CDF��S��CEB��S����EBDF�ⷽ�̽�õ�x��ֵ���Ӷ��õ�D��������
(3)����AD����D��DM��x����M�������ֱ��CD�Ľ���ʽΪy=��x+2���õ�CO=OR=2�����ORC=45�㣮��֤����AQD=45�㣮ͨ�����ɶ������涨���õ�AC2+AD2= DC2�����С�CAD=90�㣬�Ӷ��С�AQD�ǵ���ֱ�����������ɵ��������ε����ʵõ�AQ=AD��ͨ��֤����QAN�ա�ADM���õ�NA��QN�ij��������õ�ON=4�����ɵõ�N����4��0������P�������Ϊx=-4��������κ������ɵõ�y��ֵ���Ӷ��õ����ۣ�
��1����![]() �У���y=0����ã�x=4����B(4��0)����x=0���ã�y=2����C(0��2)����B(4��0)��C(0��2)����
�У���y=0����ã�x=4����B(4��0)����x=0���ã�y=2����C(0��2)����B(4��0)��C(0��2)����![]() �У��ã�
�У��ã�![]() ����ã�
����ã�![]() ������κ����ı���ʽΪ��
������κ����ı���ʽΪ��![]() ��
��
(2)��D��DG��x����G����C��CF��DG��F����B��BE��CF��E����D��x��y����
��D�ڵ�����������x��0��y��0��
��B��4��0����C(0��2)����CE=OB=4��CO=BE=FG=2��EF=BG=x-4��DF=DG+FG=2-y��S��ABC=![]() AB��OC=
AB��OC=![]() ����4+1����2=5��
����4+1����2=5��
S��CBD=S��CDF��S��CEB��S����EBDF=![]() ���������x+2y=��1��
���������x+2y=��1��
��D��x��y���ڶ��κ���![]() ������
������![]() ���������
���������![]() ���ࣨx��5����x+1��=0����x=5��x=��1����ȥ����
���ࣨx��5����x+1��=0����x=5��x=��1����ȥ����
��x=5ʱ��y=![]() =��3����D��5����3����
=��3����D��5����3����
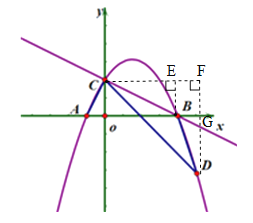
(3)��ͼ������AD����D��DM��x����M����ֱ��CD�Ľ���ʽΪy=kx+b����C��0��2����D��5����3������õ���![]() �������
�������![]() ����ֱ��CD�Ľ���ʽΪy=��x+2����y=0�������x=2����R(2��0)����CO=OR=2�����ORC=45�㣮
����ֱ��CD�Ľ���ʽΪy=��x+2����y=0�������x=2����R(2��0)����CO=OR=2�����ORC=45�㣮
�ߡ�ACO+��CAO=90�㣬��CAO+��OAD=90�㣬���ACO=��OAD�����ACO+��ADC=��OAD+��ADC=��ARC=45�㣬���AQD=45�㣮
��AC2=12+22=5��AD2=(5+1)2+32=45��DC2=52+(2+3)2=50����AC2+AD2=5+45=50= DC2�����CAD=90�㣬���QAD=90�㣮
�ߡ�AQD=45�㣬���AQD�ǵ���ֱ������������AQ=AD��
�ߡ�QAD=90�㣬���NAQ+��DAM=90�㣮
�ߡ�NAQ+��AQN=90�㣬���AQN=��MAD���ڡ�QAN�͡�ADM�У�����AQN=��MAD����QNA=��AMD=90�㣬AQ=AD�����QAN�ա�ADM����NA=DM=3��QN=AM=6����ON=4����N����4��0������P��x��y����
��QP��y�ᣬ��P�������Ϊx=-4����y=![]() =��12����PN=12����PQ=PN-QN=12��6=6��
=��12����PN=12����PQ=PN-QN=12��6=6��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CDΪ�ң���CD��AB������ΪH��
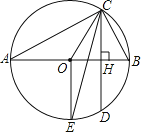
��1������BAC=30������֤��CDƽ��OB��
��2������EΪ��ADB���е㣬����0E��CE����֤��CEƽ�֡�OCD��
��3������O�İ뾶Ϊ4����BAC=30������Բ���ϵ�ֱ��AC����Ϊ3�ĵ��ж��ٸ�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�У���ľ�˺�������ڲٳ��ϣ�����ľ���������µ�Ӱ���ѻ���.
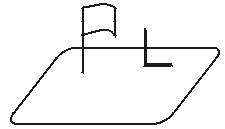
��1�����߶α�ʾ��һʱ������������µ�Ӱ��.
��2���Ƚ������ľ��Ӱ�ӵij���.
��3��ͼ���Ƿ���������������Σ�
��4��Ϊ�˳������������������Σ�ľ�˲����Է���ͼ�е���Щλ�ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y��ax2+bx+3������A��3��0���͵�B��4��3����
��1������������������Ӧ�Ķ��κ����ı���ʽ��
��2��ֱ��д���������߿��ڷ���Ͷ������꣮
��3��ֱ������������ƽ���ڻ������������ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ����OΪ��ABD�����ģ���CΪֱ��BD�·���BCD��һ�㣬�Ҳ����B��D�غϣ���ACB=��ABD=45���������ж�AC��BC��CD֮���������ϵ�ж���ȷ���ǣ� ��
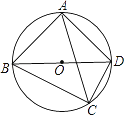
A. AC=BC+CD B. ![]() AC=BC+CD C.
AC=BC+CD C. ![]() AC=BC+CD D. 2AC=BC+CD
AC=BC+CD D. 2AC=BC+CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�ӳ���ѡ���ס���������Ʒ������Ʒÿ�����۱ȼ���Ʒÿ��������20Ԫ������������Ʒ5��������Ʒ4������Ҫ1000Ԫ��
(1)��ס���������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
(2)��������Ʒ���ۼ�Ϊÿ��145Ԫ��������Ʒ���ۼ�Ϊÿ��120Ԫ�����̵��������ס���������Ʒ��40��������������Ʒȫ���۳�������������870Ԫ���������Ʒ���ٿɹ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̵�8�·�Ӫҵ��Ϊ15��Ԫ,9�·��½���20%���ܡ�ʮһ���ƽ����Լ������������ص�Ӱ��,10�·ݡ�11�·�Ӫҵ�������һ������������,10�·���������11�·������ʵ�1.5��,��֪�������̵�11�·�Ӫҵ��Ϊ24��Ԫ��
��1���ʣ�9�·ݵ�Ӫҵ���Ƕ�����Ԫ��
��2����10�·�Ӫҵ��������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�п�չ�Ļ������Ż�У�ij����С��Ҫ��һ�鿿ǽ��ǽ��15�ף��Ŀյ�����һ�����λ�ABCD������һ�߿�ǽ�����������ܳ�Ϊ40m��դ��Χ�ɣ����軨ƽ����ǽ��һ�߳�Ϊx��m�����������Ϊy��m2����
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2�����������Ļ�����ܴﵽ200m2�����ܣ������ʱx��ֵ�������ܣ�˵�����ɣ�
��3�����ݣ�1������õĺ�����ϵʽ���жϵ�xȡ��ֵʱ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=6��BC=4����E�DZ�BC��һ���㣬����DCE��DE�۵�����DFE������DF��ֱ��CB�ڵ�P������AFDΪ����������ʱ��DP�ij�Ϊ_____��
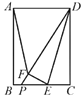
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com