
【题目】如图,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
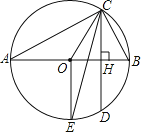
(1)若∠BAC=30°,求证:CD平分OB.
(2)若点E为弧ADB的中点,连接0E,CE.求证:CE平分∠OCD.
(3)若⊙O的半径为4,∠BAC=30°,则圆周上到直线AC距离为3的点有多少个?请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)2,理由见解析.
【解析】
试题(1)根据圆周角定理由AB为⊙O的直径得到∠ACB=90°,而∠BAC=30°,所以∠B=60°,于是可判断△OBC为等边三角形,根据等边三角形的性质由CD⊥OB易得CD平分OB;
(2)由点E为![]() 的中点,根据垂径定理的推论得OE⊥AB,则OE∥CD,根据平行线的性质得∠OEC=∠ECD,而∠OEC=∠OCE,所以∠OCE=∠ECD;
的中点,根据垂径定理的推论得OE⊥AB,则OE∥CD,根据平行线的性质得∠OEC=∠ECD,而∠OEC=∠OCE,所以∠OCE=∠ECD;
(3)作OF⊥AC于F,交⊙O于G,根据含30度的直角三角形三边的关系得OF=![]() OA=2,则GF=OG-OF=2,于是可得到在弧AC上没有一个点到AC的距离为3cm,在弧AEC上有两个点到AC的距离为3cm.
OA=2,则GF=OG-OF=2,于是可得到在弧AC上没有一个点到AC的距离为3cm,在弧AEC上有两个点到AC的距离为3cm.
试题解析:(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴∠B=60°,
而OC=OB,
∴△OBC为等边三角形,
∵CD⊥OB,
∴CD平分OB;
(2)证明:∵点E为![]() 的中点,
的中点,
∴OE⊥AB,
而CD⊥AB,
∴OE∥CD
∴∠OEC=∠ECD,
∵OC=OE,
∴∠OEC=∠OCE,
∴∠OCE=∠ECD,
即CE平分∠OCD;
(3)圆周上到直线AC距离为3的点有2个.理由如下:
作OF⊥AC于F,交⊙O于G,如图,
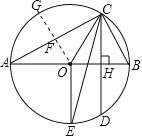
∵OA=4,∠BAC=30°,
∴OF=![]() OA=2,
OA=2,
∴GF=OG-OF=2,即在![]() 上到AC的最大距离为2cm,
上到AC的最大距离为2cm,
∴在![]() 上没有一个点到AC的距离为3cm,
上没有一个点到AC的距离为3cm,
而在![]() 上到AC的最大距离为6cm,
上到AC的最大距离为6cm,
∴在![]() 上有两个点到AC的距离为3cm.
上有两个点到AC的距离为3cm.
考点: 圆的综合题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
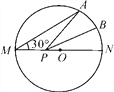
【题目】如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
A. 4![]() B. 2 C. 4 D. 2
B. 2 C. 4 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
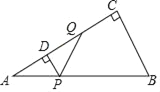
【题目】如图,E、F分别是 四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,记S1=S△APD,S2=S△BQC,四边形EQFP的面积为S.
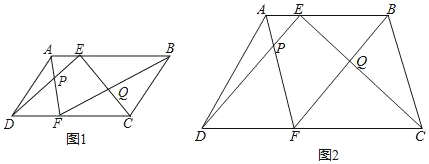
(1)若四边形ABCD为平行四边形,如图1,求证:S=S1+S2;
(2)若四边形ABCD为一般凸多边形,AB∥CD,如图2,求证:S=S1+S2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数表示即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
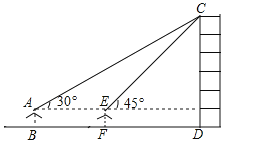
【题目】(7分)小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:![]() ,
,![]() .结果保留整数)
.结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
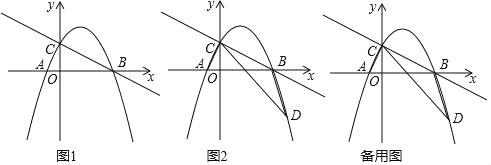
【题目】在平面直角坐标系中,直线y=﹣![]() x+2与x轴交于点B,与y轴交于点C,二次函数y=﹣
x+2与x轴交于点B,与y轴交于点C,二次函数y=﹣![]() +bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
(1)求二次函数的表达式;
(2)如图1,点D是抛物线第四象限上的一动点,连接DC,DB,当S△DCB=S△ABC时,求点D坐标;
(3)如图2,在(2)的条件下,点Q在CA的延长线上,连接DQ,AD,过点Q作QP∥y轴,交抛物线于P,若∠AQD=∠ACO+∠ADC,请求出PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com