
【题目】已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( )
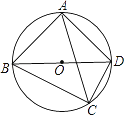
A. AC=BC+CD B. ![]() AC=BC+CD C.
AC=BC+CD C. ![]() AC=BC+CD D. 2AC=BC+CD
AC=BC+CD D. 2AC=BC+CD
【答案】B
【解析】
在CD延长线上截取DE=BC,连接EA,证明△ABC≌△ADE,进而得到△CAE是等腰直角三角形,即可得出结论.
在CD的延长线上截取DE=BC,连接EA,
∵∠ABD=∠ACB=∠ABD=45°,
∴AB=AD,
∵∠ADE+∠ADC=180°,
∠ABC+∠ADC=180°,
∴∠ABC=∠ADE,
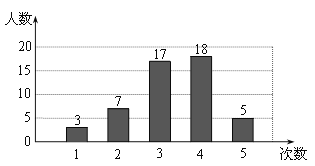
在△ABC与△ADE中,
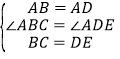 ,
,
∴△ABC≌△ADE(SAS),
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE=90°,
∴∠ACD=∠ABD=45°,
∴△CAE是等腰直角三角形,
∴AC=AE,AC2+AE2=CE2,
∴ ![]() AC=CE,
AC=CE,
∴ ![]() AC=CD+DE=CD+BC,
AC=CD+DE=CD+BC,
故选B.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数表示即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“学雷锋社会实践”活动中,某校为了解全校1200名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成条形统计图如下:
(Ⅰ)求这50个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估算该校1200名学生共参加了多少次活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(-1,0),将△ABO绕点O顺时针旋转,若点A的对应点A′的坐标为(2,0),
(1)则点B的对应点B′的坐标为_____;
(2)画出旋转后的图形.
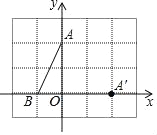
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
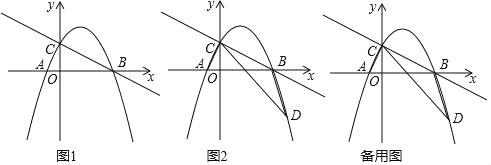
【题目】在平面直角坐标系中,直线y=﹣![]() x+2与x轴交于点B,与y轴交于点C,二次函数y=﹣
x+2与x轴交于点B,与y轴交于点C,二次函数y=﹣![]() +bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A.
(1)求二次函数的表达式;
(2)如图1,点D是抛物线第四象限上的一动点,连接DC,DB,当S△DCB=S△ABC时,求点D坐标;
(3)如图2,在(2)的条件下,点Q在CA的延长线上,连接DQ,AD,过点Q作QP∥y轴,交抛物线于P,若∠AQD=∠ACO+∠ADC,请求出PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
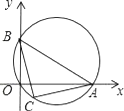
【题目】如图,点A,B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是![]() 的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的是_________(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 |
摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
摸到黑球的频率 |
|
|
|
| a |
![]() 表中a的值等于______;
表中a的值等于______;
![]() 估算口袋中白球的个数;
估算口袋中白球的个数;
![]() 用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com