


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
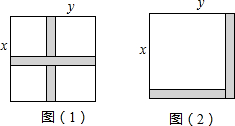 如图(1)、(2)某小区规划在边长为x米的正方形场地上修建两条宽为y米的人行道,其余部分种草,请你用不同的方法表示出草坪所占的面积,从中你发现了什么数学公式?请写出来.
如图(1)、(2)某小区规划在边长为x米的正方形场地上修建两条宽为y米的人行道,其余部分种草,请你用不同的方法表示出草坪所占的面积,从中你发现了什么数学公式?请写出来.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1). 我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”为一次变换.
如图,在平面直角坐标系xOy中,正方形ABCD顶点A(-1,-1)、B(-3,-1). 我们规定“把正方形ABCD先沿x轴翻折,再向右平移2个单位”为一次变换.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 22 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 32 |
| 1 |
| 9 |
| 8 |
| 9 |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 42 |
| 1 |
| 16 |
| 15 |
| 16 |
| 3 |
| 4 |
| 5 |
| 4 |
| 1 |
| 52 |
| 1 |
| 25 |
| 24 |
| 25 |
| 4 |
| 5 |
| 6 |
| 5 |
| 1 |
| 102 |
| 1 |
| 1002 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20122 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com