Question

已知点P为正方形ABCD所在平面上的一点，且AP=AD，连接AP、BP、DP，则∠BPD的度数等于________．

Answer 1

45°或135°
分析：①P在正方形ABCD内时，求出AB=AP=AD，∠BAD=90°，推出∠ABP=∠APB，∠APD=∠ADP，求出2∠APB+2∠APD=180°-∠BAP+180°-∠DAP=270°，即可求出∠BPD即可；
②P在正方形ABCD外时，∠PAD为锐角时，求出AB=AD，∠BAD=90°，AP=AD，推出∠ABP=∠APB，∠ADP=∠APD，推出∠BAD=2∠BPD，求出∠BPD即可；当∠P′AD为钝角时，求出∠AP′D=∠ADP′，∠AP′B=∠ABP′，根据三角形内角和定理求出2（∠AP′D+∠AP′B）+45°+45°=180°，即可求出∠BP′D．
解答：有两种情况：
①P在正方形ABCD内时，如图：
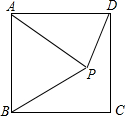
∵正方形ABCD，AP=AD，
∴AB=AP=AD，∠BAD=90°，
∴∠ABP=∠APB，∠APD=∠ADP，
∵∠BAP+∠ABP+∠APB=180°，∠ADP+∠APD+∠DAP=180°，
∴2∠APB+2∠APD=180°-∠BAP+180°-∠DAP=180°+180°-90°=270°，
∴∠BPD=135°；
②P在正方形ABCD外时，如图：
有2点，
∠PAD为锐角时，
∵ABCD是正方形，
∴AB=AD，∠BAD=90°，AP=AD，
∴∠ABP=∠APB，∠ADP=∠APD，
∴∠PAD=180°-2∠APD=180°-2∠APB-2∠BPD，
∠BAD+∠PAD=∠BAP=180°-2∠APB，
相减得：∠BAD=2∠BPD，
∴∠BPD=45°；
当∠P′AD为钝角时，
∵由正方形ABCD得出∠ABD=∠ADB=45°，AB=AD=AP，
∴∠AP′D=∠ADP′，∠AP′B=∠ABP′，
∴∠AP′D+∠AP′B+∠ABP′+∠ABD+∠ADB+∠ADP′=180°，
∴2（∠AP′D+∠AP′B）+45°+45°=180°，
∴∠BP′D=45°；
故答案为：45°或135°．
点评：本题考查了正方形性质，等腰三角形性质，三角形的内角和定理等知识点的应用，主要考查学生运用性质进行推理的能力，用了分类讨论思想，本题有一定的难度，对学生提出了较高的要求．