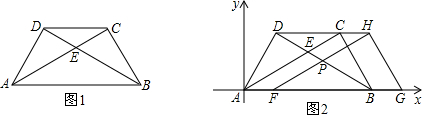
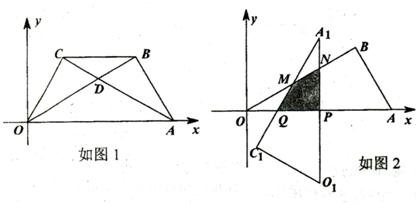
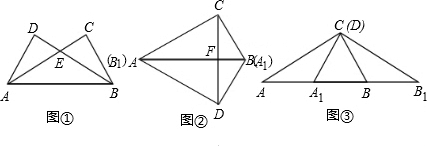
解:(1)∵在Rt△ABC和Rt△ABD中,∠BAC=∠DBA=30°,AB=8,
∴A、B、C、D四点的坐标分别是:(0,0)、(8,0)、(6,

)、(2,

),
设:过A、B、C、D四点的抛物线的解析式为:y=a(x-x
1)(x-x
2),
∵A、B两点坐标为(0,0)、(8,0),
∴解析式为:y=a(x-0)(x-8)=ax(x-8),
∵D点的坐标是:(2,

),
∴代入解析式得:

=2a(2-8),
解得
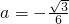
,
∴解析式为:
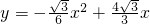
,
∵C点坐标是(6,

),
把x=6代入解析式得:
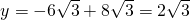
,
∴C点在过A、B、D三点的抛物线上,
∴过A、B、C、D四点的抛物线的解析式是
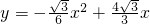
.
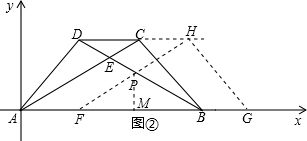
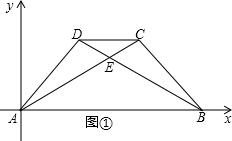
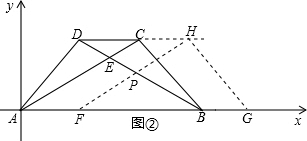
(2)如图,
过点P做PM⊥AB垂足为M,
∴∠PMF=90°
在△FHG中,∠GHF=90°,∠GFH=30°,FG=8,
∴HG=4,
∴根据勾股定理得:
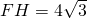
,
∵∠PMF=∠GHF=90°,∠HFG=∠MFP=30°,
∴△HFG∽△MFP,
∴
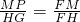
,
∵∠PFM=∠PBM=30°,
∴PF=PB,
∵PM⊥AB,
∴
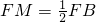
,
∵AF=x,AB=8,
∴FB=8-x,
∴
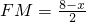
,
由
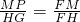
可知,
.
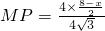
=

,
∴
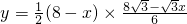
,
即:

∴y与x的函数关系式为:

.
分析:(1)利用有一角是30°的直角三角形的特性和勾股定理,求出A、B、C、D四点的坐标,利用A、B两点设出两点式解析式,代入C点求出,再代入D点验证,也可代入D点求出,用C点验证;
(2)作PM⊥AB,进一步利用有一角是30°的直角三角形的特性和勾股定理,用x表示出BF,再利用△HFG∽△MFP,用x表示出PM,最后运用三角形的面积求得.
点评:本题考查了二次函数解析式的确定、图形面积的求法、勾股定理、相似三角形的判定和性质等知识点.

 )、(2,
)、(2, ),
), ),
), =2a(2-8),
=2a(2-8),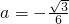 ,
,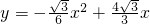 ,
, ),
),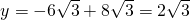 ,
,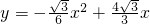 .
.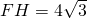 ,
,
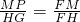 ,
,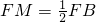 ,
,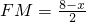 ,
,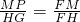 可知,
可知,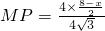 =
= ,
,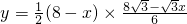 ,
,
 .
.

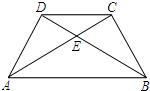 C=AD=4,AC与BD相交于点E,连接CD.
C=AD=4,AC与BD相交于点E,连接CD.