
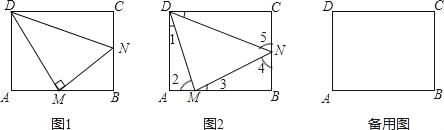
【题目】如图,矩形ABCD中,点M从A点出发在线段AB上作匀速运动(不与A、B重合),同时点N从B点出发在线段BC上作匀速运动.
(1)如图1,若M为AB中点,且DM⊥MN.请在图中找出两对相似三角形:
① ∽ _,② ∽ ,选择其中一对加以证明;
(2)①如图2,若AB=5,BC=3点M的速度为1个单位长度/秒,点N的速度为![]() 个单位长度/秒,运动的时间为t秒.当t为何值时,△DAM与△MBN相似?请说明理由;
个单位长度/秒,运动的时间为t秒.当t为何值时,△DAM与△MBN相似?请说明理由;
②如果把点N的速度改为a个单位长度/秒,其它条件不变,是否存在a的值,使得△DAM与△MBN和△DCN这两个三角形都相似?若存在,请求出a的值;若不存在,请说明理由.
【答案】(1)详见解析;(2)①当t=![]() 时,△DAM∽△MBN;当t=
时,△DAM∽△MBN;当t=![]() ﹣3时,△DAM∽△NBM;②当a=
﹣3时,△DAM∽△NBM;②当a=![]() 时,△DAM∽△MBN∽△DCN.
时,△DAM∽△MBN∽△DCN.
【解析】分析:(1)首先可得有△DAM∽△MBN,△DAM∽△DMN,△DMN∽△MBN三对相似;然后选择其中的一对证明即可,注意应用矩形的性质,特别是同角或等角的余角相等的性质的应用;
(2)①如图2可得AM=t,MB=5﹣t,BN=![]() t(0<t<5),然后分两种情况:(Ⅰ)当∠1=∠3时,△DAM∽△MBN;(Ⅱ)当∠2=∠3时,△DAM∽△NBM去分析根据相似三角形的对应边成比例,即可得方程,解方程即可求得答案;
t(0<t<5),然后分两种情况:(Ⅰ)当∠1=∠3时,△DAM∽△MBN;(Ⅱ)当∠2=∠3时,△DAM∽△NBM去分析根据相似三角形的对应边成比例,即可得方程,解方程即可求得答案;
②分四种情况去分析:(Ⅰ)当∠1=∠3=∠6时,∠DMN=90°,△DAM∽△MBN∽△DCN,(Ⅱ)当∠1=∠3=∠5时,(Ⅲ)当∠2=∠3=∠6时,(Ⅳ)当∠2=∠3=∠5时,△DAM∽△NBM∽△DCN,根据相似三角形的对应边成比例列方程求解即可求得答案.
详解:(1)有△DAM∽△MBN,△DAM∽△DMN,△DMN∽△MBN三对相似;
选△DAM∽△MBN,证明:∵四边形ABCD是矩形,∴∠A=∠B=90°,∴∠ADM=90°﹣∠AMD.∵DM⊥MN,∴∠BMN=180°﹣90°﹣∠AMD=90°﹣∠AMD,∴∠ADM=∠BMD,∴△DAM∽△MBN;
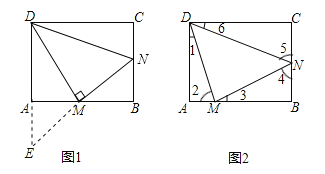
选△DAM∽△DMN,证明:延长NM交DA的延长线于E点,如图1.
∵四边形ABCD是矩形,∴∠DAB=∠B=90°,∴∠EAM=∠B=90°.又∵∠AME=∠BMN,AM=BM,∴△AME≌△BMN,∴EM=MN.又∵DM⊥MN,∴DE=DN,∴∠ADM=∠NDM.又∵∠DAM=∠DMN=90°,∴△DAM∽△DMN;
选△DAM∽△MBN,证明:延长MN交DA的延长线于E点,如图1.
∵四边形ABCD是矩形,∴∠DAB=∠B=90°,∴∠EAM=∠B=90°.又∵∠AME=∠BMN,AM=BM,∴△AME≌△BMN,∴EM=MN,∠E=∠MNB.又∵DM⊥MN,∴DE=DN,∴∠E=∠DNM,∴∠DNM=∠MNB.又∵∠DMN=∠B=90°,∴△DMN∽△MBN;
(2)①如图2,AM=t,MB=5﹣t,BN=![]() t(0<t<5),分两种情况:
t(0<t<5),分两种情况:
(Ⅰ)当∠1=∠3时,△DAM∽△MBN,∴![]() ,解得:t=
,解得:t=![]() 。
。
(Ⅱ)当∠2=∠3时,△DAM∽△NBM,∴![]() ,∴AMBN=ADBM,∴t×
,∴AMBN=ADBM,∴t×![]() t=3(5﹣t),解得:t3=
t=3(5﹣t),解得:t3=![]() ﹣3,t4=﹣
﹣3,t4=﹣![]() ﹣3(不合题意舍去)。
﹣3(不合题意舍去)。
∴当t=![]() 时,△DAM∽△MBN;当t=
时,△DAM∽△MBN;当t=![]() ﹣3时,△DAM∽△NBM.
﹣3时,△DAM∽△NBM.
②分四种情况:(Ⅰ)当∠1=∠3=∠6时,∠DMN=90°,△DAM∽△MBN∽△DCN,由![]() ,得:BN=
,得:BN=![]() ,∴CN=
,∴CN=![]() ,由
,由![]() ,得:CNMB=DCBN,∴
,得:CNMB=DCBN,∴![]() ﹣(5﹣t)=5﹣
﹣(5﹣t)=5﹣![]() ,化简得:t2﹣10t+9=0,解得:t1=1,t2=9(不合题意舍去),a=
,化简得:t2﹣10t+9=0,解得:t1=1,t2=9(不合题意舍去),a=![]() ;
;
(Ⅱ)当∠1=∠3=∠5时.∵∠5+∠6=90°,∴∠1+∠6=90°,(与已知条件矛盾), 所以此时不存在.
(Ⅲ)当∠2=∠3=∠6时,方法一:∵∠1+∠2=90°,∴∠1+∠6=90°,(与已知条件矛盾)所以此时不存在.
方法二:由![]() ,得:BN=
,得:BN=![]() ,∴CN=
,∴CN=![]() ,由
,由![]() ,得:CNMB=DCBN,∴
,得:CNMB=DCBN,∴![]() (5﹣t)=5﹣
(5﹣t)=5﹣![]() ,解得:t=5(不合题意舍去),所以此时不存在.
,解得:t=5(不合题意舍去),所以此时不存在.
(Ⅳ)当∠2=∠3=∠5时,△DAM∽△NBM∽△DCN,由(Ⅲ)得BN=![]() ,∴CN=
,∴CN=![]() ,由
,由![]() ,得:CNNB=DCBM,∴
,得:CNNB=DCBM,∴![]() ﹣
﹣![]() =5(5﹣t),化简得:5t2﹣18t+45=0方程没有实数根,所以此时不存在.
=5(5﹣t),化简得:5t2﹣18t+45=0方程没有实数根,所以此时不存在.
综上所述:当a=![]() 时,△DAM∽△MBN∽△DCN.
时,△DAM∽△MBN∽△DCN.


科目:初中数学 来源: 题型:
【题目】某商贩在批发市场以每包![]() 元的价格购进甲种茶叶40包,以每包
元的价格购进甲种茶叶40包,以每包![]() 元的价格购进乙种茶叶60包.
元的价格购进乙种茶叶60包.
(1)该商贩购进甲、乙两种茶叶共需资金______元(用含![]() ,
,![]() 的式子表示);
的式子表示);
(2)若该商贩将两种茶叶都提价![]() 全部售出,共可获利多少元(用含
全部售出,共可获利多少元(用含![]() ,
,![]() 的式子表示)?
的式子表示)?
(3)若该商贩将两种茶叶都以每包![]() 元的价格全部出售,在这次买卖中该商贩是盈利还是亏损,请说明理由.
元的价格全部出售,在这次买卖中该商贩是盈利还是亏损,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
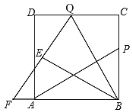
【题目】如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
(1)试探究AP与BQ的数量与位置关系,并证明你的结论;
(2)当E是FQ的中点时,求BP的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在△ABC中,AC=3,BC=6,∠C=60![]() ;
;
(1)将△ABC绕着点C旋转,使点A落在直线BC上的点A′,点B落在B′,在下图中画出旋转后的△A′B′C.
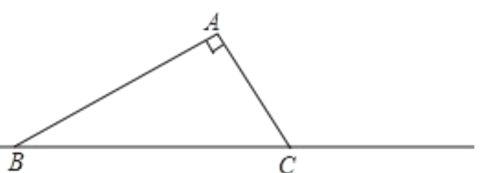
(2)直接写出A′B的长,A′B=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
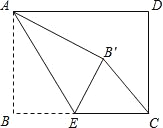
A. 3 B. ![]() C. 2或3 D. 3或
C. 2或3 D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,在直线AB同侧任作射线OC、OD,使得∠COD=90°
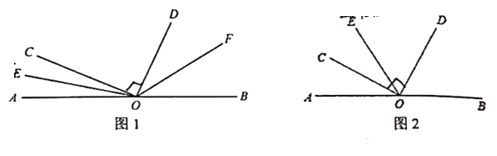
(1)如图1,过点O作射线OE,当OE恰好为∠AOC的角平分线时,另作射线OF,使得OF平分∠BOD,则∠EOF的度数是__________度;
(2)如图2,过点O作射线OE,当OE恰好为∠AOD的角平分线时,求出∠BOD与∠COE的数量关系;
(3)过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,若∠EOC=3∠EOF,直接写出∠AOE的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位采购员同时去一家饲料公司买两次饲料,两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料,购买的饲料单价分别为m元/千克和n元/千克,
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为( )
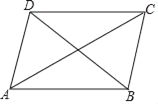
A. α B. ![]() C. 90﹣α D. 90﹣
C. 90﹣α D. 90﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com