
| A. | ∠A+∠B=∠C | B. | ∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C | C. | ∠A:∠B:∠C=1:2:3 | D. | ∠A=2∠B=3∠C |
分析 由直角三角形内角和为180°求得三角形的每一个角的度数,再判断其形状即可.
解答 解:A、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴2∠C=180°,解得∠C=90°,∴△ABC是直角三角形,∴本选项错误;
B、设∠A=x,∠B=2x,∠C=3x,∵∠A+∠B+∠C=180°,∴x+2x+3x=180°,解得x=30°,∴∠C=90°,∴本选项错误;
C、设∠A=x,∠B=2x,∠C=3x,∵∠A+∠B+∠C=180°,∴x+2x+3x=180°,解得x=30°,∴∠C=90°,∴本选项错误;
D、∵∠A+∠B+∠C=180°,而∠A=2∠B=3∠C,∴3∠C+$\frac{3}{2}$∠C+∠C=180°,解得∠C=$\frac{360°}{11}$,∴∠A=3∠C=$\frac{1080°}{11}$,∴本题选项正确.
故选D.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
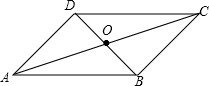 如图,在?ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△AOB的周长为( )
如图,在?ABCD中,对角线AC,BD相交于点O,若AC=14,BD=8,AB=10,则△AOB的周长为( )| A. | 32 | B. | 24 | C. | 21 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
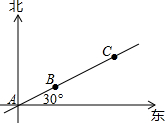 如图,A,B,C三人的位置在同一直线上,AB=5米,BC=10米,下列说法正确的是( )
如图,A,B,C三人的位置在同一直线上,AB=5米,BC=10米,下列说法正确的是( )| A. | C在A的北偏东30°方向的15米处 | B. | A在C的北偏东60°方向的15米处 | ||
| C. | C在B的北偏东60°方向的10米处 | D. | B在A的北偏东30°方向的5米处 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $±\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x3+x3=x6 | B. | (2x+1)2-(2x-1)2=4x | C. | (2ab2)3=2a2b6 | D. | a4n÷a2n=a2n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}÷\sqrt{2}=9$ | B. | ${(\frac{1}{3})}^{-2}=\frac{1}{9}$ | C. | (-a2)3=a6 | D. | a6÷($\frac{1}{2}$a2)=2a4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
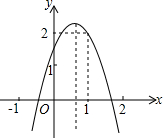 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上)
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com