
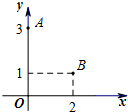
 如图所示,A、B两点的坐标分别为(0,3)、(2,1),点C是x轴上一点,且三角形ABC的面积为3,则点C的坐标为(0,0)或(6,0).
如图所示,A、B两点的坐标分别为(0,3)、(2,1),点C是x轴上一点,且三角形ABC的面积为3,则点C的坐标为(0,0)或(6,0). 分析 根据图象求出AB,利用待定系数法求出过点A,B的直线的函数解析式,再根据点到直线的距离求出点C到直线AB的距离,根据面积公式,即可解答.
解答 解:由图象可得:A(3,0),B(2,1),
AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
设过点A,B的直线的函数解析式为:y=kx+b,
把点A(3,0),B(2,1)代入可得:$\left\{\begin{array}{l}{3k+b=0}\\{2k+b=1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
则过点A,B的直线的函数解析式为:y=-x+3,
设点C的坐标为(x,0),
则点C到直线AB的距离为:|$\frac{-x+3}{\sqrt{(-1)^{2}+(-1)^{2}}}$|=$\frac{|-x+3|}{\sqrt{2}}$,
∵三角形ABC的面积为3,
∴$\frac{1}{2}×2\sqrt{2}×\frac{|-x+3|}{\sqrt{2}}$=3,
|-x+3|=3,
解得:x=0或x=6,
∴点C的坐标为(0,0)或(6,0).
故答案为:(0,0)或(6,0).
点评 本题考查了图形与坐标,解决本题的关键是求出点C到直线AB的距离.


科目:初中数学 来源: 题型:填空题
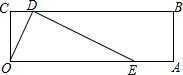 如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.
如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
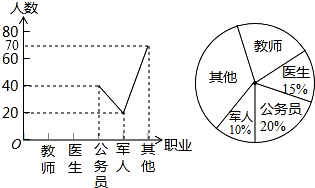
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查初三某班体育模拟考试成绩的满分率 | |
| B. | 调查某类烟花爆竹燃放安全情况 | |
| C. | 调查某品牌牛奶的质量合格情况 | |
| D. | 调查全国中学生对“雾霾”的了解情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com