练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知2x6y2和-$\frac{1}{2}{x^{3m}}{y^n}$是同类项，那么2m+n的值是（　　）
    A．2B．4C．6D．5

    分析 依据同类项的蒂尼可知3m=6，n=2，从而得到m=2，然后代入计算即可．

    解答 解：∵2x6y2和-$\frac{1}{2}{x^{3m}}{y^n}$是同类项，
    ∴3m=6，n=2．
    ∴m=2．
    将m=2，n=2代入得：原式=2×2+2=6．
    故选：C．

    点评 本题主要考查的是同类项的定义，由同类项的定义得到3m=6，n=2是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．计算：（-1）4-（1-0.5×$\frac{1}{3}$）×6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．单项式-3xny2是5次单项式，则n=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

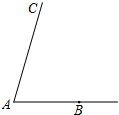    17．如图，已知∠CAB，用直尺和圆规作∠ABD，使∠ABD=$\frac{1}{2}$∠A，射线BD与射线AC相交于点D．（不写画法，保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．当x=0时，分式$\frac{x}{x-1}$值为0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

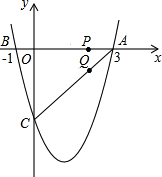    5．如图，二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A（3，0），B（-1，0），与y轴交于点C．若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动．
    （1）求该二次函数的解析式及点C的坐标；
    （2）当P，Q运动t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定此时四边形APDQ的形状并求说明理由；
    （3）当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A，E，Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知如图，AC、BD相交于点O，且被点O互相平分，求证：
    （1）AB∥CD；
    （2）AB=CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

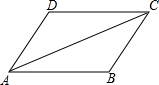    9．用2根同样长的木条AB，CD和另外两根同样长的木条AD，BC拼成一个四边形ABCD，
    （1）连接AC，△ABC≌△CDA么？
    （2）求证：AB∥CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

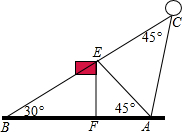    10．如图，某校20周年校庆时，需要在草场上利用气球悬挂宣传条幅，EF为旗杆，气球从A处起飞，几分钟后便飞达C处，此时，在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上．
    （1）已知旗杆高为12米，若在点B处测得旗杆顶点E的仰角为30°，A处测得点E的仰角为45°，试求AB的长（结果保留根号）；
    （2）在（1）的条件下，若∠BCA=45°，绳子在空中视为一条线段，试求绳子AC的长（结果保留根号）？

    查看答案和解析>>

    同步练习册答案