
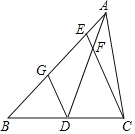
【题目】如图,△ABC中,AD是BC边上的中线,点E在AB边上,且![]() =
=![]() ,CE交AD于点F,点G是BE中点,若△ABC的面积为112,则△AEF的面积为_______.
,CE交AD于点F,点G是BE中点,若△ABC的面积为112,则△AEF的面积为_______.
【答案】2
【解析】
由三角形的中线性质得出△ACD的面积=![]() △ABC的面积=56,证出DG是△BCE的中位线,得出DG∥CE,DG=
△ABC的面积=56,证出DG是△BCE的中位线,得出DG∥CE,DG=![]() CE,证出△AEF∽△AGD,得出
CE,证出△AEF∽△AGD,得出![]() =
=![]() =
=![]() =
=![]() ,求出△ACF的面积=
,求出△ACF的面积=![]() △AD的面积=14,证出
△AD的面积=14,证出![]() =
=![]() ,即可得出答案.
,即可得出答案.
解:∵AD是BC边上的中线,△ABC的面积为112,
∴△ACD的面积=![]() △ABC的面积=56,
△ABC的面积=56,
∵点G是BE中点,
∴BG=EG,DG是△BCE的中位线,
∴DG∥CE,DG=![]() CE,
CE,
∴△AEF∽△AGD,
∴![]() =
=![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴△ACF的面积=![]() △ACD的面积=14,
△ACD的面积=14,
∵![]() =
=![]() ,DG=
,DG=![]() CE,
CE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴△AEF的面积=![]() △ACF的面积=
△ACF的面积=![]() ×14=2;
×14=2;
故答案为:2.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
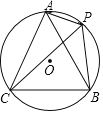
【题目】如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:PA+PB=PC;
(2)若BC=![]() ,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中对 600 名毕业生中考体育测试坐位体前屈成绩进行整理,绘制成 如下不完整的统计图:
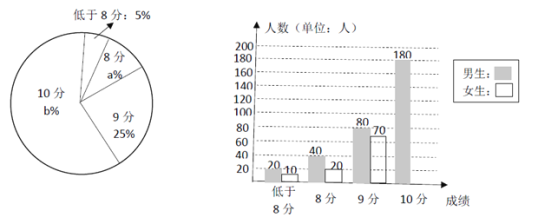
根据统计图,回答下列问题。
(1)请将条形统计图补充完整;
(2)扇形统计图中,b= ,得 8 分所对应扇形的圆心角度数为 ;
(3)在本次调查的学生中,随机抽取 1 名男生,他的成绩不低于 9 分的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸是一家水果店的经理.一天,他去水果批发市场,用100元购进甲种水果,用100元购进乙种水果,已知乙种水果比甲种水果多10千克,乙种水果的批发价比甲种水果的批发价低0.5元.
(1)求甲、乙两种水果各购进了多少千克?
(2)如果当天甲、乙两种水果都按2.80元出售,乙种水果很快售完,而甲种水果先售出![]() ,剩余的按售价打5折售完.请你通过计算,说明这一天的水果买卖是否赚钱?如果赚钱,赚了多少元?如果不赚钱,那么赔了多少元?
,剩余的按售价打5折售完.请你通过计算,说明这一天的水果买卖是否赚钱?如果赚钱,赚了多少元?如果不赚钱,那么赔了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
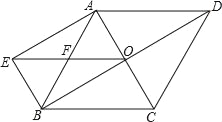
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
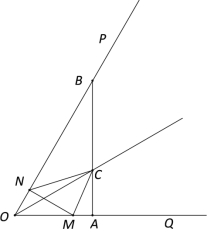
【题目】如图,已知∠POQ=60°,点A、B分别在射线OQ、OP上,且OA=2,OB=4,∠POQ的平分线交AB于C,一动点N从O点出发,以每秒1个单位长度的速度沿射线OP向点B作匀速运动,MN⊥OB交射线OQ于点M.设点N运动的时间为t(0<t<2)秒.
(1)求证:△ONM∽△OAB;
(2)当MN=CM时,求t的值;
(3)设△MNC与△OAB重叠部分的面积为S.请求出S关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com