
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地. 
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 , 为什么?
【答案】
(1)解:设所围矩形ABCD的长AB为x米,则宽AD为 ![]() (80﹣x)米.
(80﹣x)米.
依题意,得x ![]() (80﹣x)=750.
(80﹣x)=750.
即,x2﹣80x+1500=0,
解此方程,得x1=30,x2=50.
∵墙的长度不超过45m,∴x2=50不合题意,应舍去.
当x=30时, ![]() (80﹣x)=
(80﹣x)= ![]() ×(80﹣30)=25,
×(80﹣30)=25,
所以,当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2
(2)解:不能.
因为由x ![]() (80﹣x)=810得x2﹣80x+1620=0.
(80﹣x)=810得x2﹣80x+1620=0.
又∵b2﹣4ac=(﹣80)2﹣4×1×1620=﹣80<0,
∴上述方程没有实数根.
因此,不能使所围矩形场地的面积为810m2
【解析】(1)设所围矩形ABCD的长AB为x米,则宽AD为 ![]() (80﹣x)米,根据矩形面积的计算方法列出方程求解.(2)假使矩形面积为810,则x无实数根,所以不能围成矩形场地.
(80﹣x)米,根据矩形面积的计算方法列出方程求解.(2)假使矩形面积为810,则x无实数根,所以不能围成矩形场地.


科目:初中数学 来源: 题型:
【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D , CE是△ABC的角平分线.
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( ) 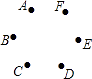
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,…,如此作下去,则△B2014A2015B2015的顶点A2015的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AE等于弧AB,BE分别交AD、AC于点F、G. 
(1)判断△FAG的形状,并说明理由;
(2)若点E和点A在BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变,(1)中的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形 OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1,![]() ),则点C 的坐标为( )
),则点C 的坐标为( )

A. (﹣1,![]() ) B. (
) B. (![]() ,1) C. (
,1) C. (![]() ,3) D. (
,3) D. (![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F分别在BC、AB、AC上. 
(1)若设AE=x,则AF=;(用含x的代数式表示)
(2)要使剪出的矩形CDEF的面积最大,点E应选在何处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威远人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com