Question

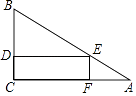
【题目】一块三角形材料如图所示，∠A=30°，∠C=90°，AB=12，用这块材料剪出一个矩形CDEF，其中D、E、F分别在BC、AB、AC上．
（1）若设AE=x，则AF=；（用含x的代数式表示）
（2）要使剪出的矩形CDEF的面积最大，点E应选在何处？

Answer 1

【答案】
（1） x
（2）解：∵四边形CDEF是矩形，

∴∠AFE=90°，

∵∠A=30°，

∴EF= AE= x，

在Rt△ABC中，∠C=90°，AB=12，

∴BC= AB=6，

根据勾股定理得：AC= =6 ，

∴CF=AC﹣AF=6 ﹣ x，

∴S矩形CDEF=CFEF= x（6 ﹣ x）=﹣ （x﹣6）2+9 ，

∴当x=6时，矩形CDEF的面积最大，

即当点E为AB的中点时，矩形CDEF的面积最大．

【解析】解：（1）在Rt△ABC中，∠A=30°，∠C=90°，AE=x， ∴EF= x，根据勾股定理得：AF= x；所以答案是： x；
【考点精析】根据题目的已知条件，利用二次函数的最值和矩形的性质的相关知识可以得到问题的答案，需要掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；矩形的四个角都是直角，矩形的对角线相等．