
【题目】如图,已知△ABC中,∠B=∠C,AB=AC=10cm,BC=8cm,点D为AB的中点.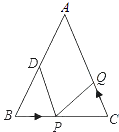
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC边上相遇?
【答案】
(1)解:①∵t=1s,
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中, 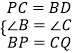 ,
,
∴△BPD≌△CQP(SAS).
②∵vP≠vQ ,
∴BP≠CQ,
若△BPD≌△CPQ,∠B=∠C,
则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间 ![]() ,
,
∴ ![]() cm/s
cm/s
(2)解:设经过x秒后点P与点Q第一次相遇,
由题意,得 ![]() x=3x+2×10,
x=3x+2×10,
解得 ![]() .
.
∴点P共运动了 ![]() ×3=80cm.
×3=80cm.
△ABC周长为:10+10+8=28cm,
若是运动了三圈即为:28×3=84cm,
∵84﹣80=4cm<AB的长度,
∴点P、点Q在AB边上相遇,
∴经过 ![]() s点P与点Q第一次在边AB上相遇
s点P与点Q第一次在边AB上相遇
【解析】(1)①根据时间和速度分别求得BP、BD、PC、QC的长,根据SAS判定两个三角形全等.②根据全等三角形对应边相等可得到BP=PC=4cm,CQ=BD=5cm,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;(2)由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个腰长.


科目:初中数学 来源: 题型:
【题目】从A地向B地打长途,不超3分钟,收费2.4元,以后每超一分超加收一元,若通话时间为t分钟(t≥3且t是整数),则付话费y元与t分钟函数关系式是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内角∠ABC与外角∠ACD的平分线交于点E,且CE∥AB,AC与BE交于点E,则下列结论错误的是( )
A.CB=CE
B.∠A=∠ECD
C.∠A=2∠E
D.AB=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.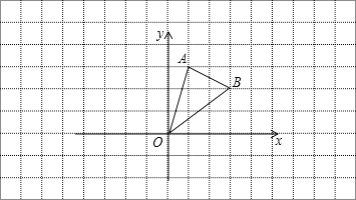
(1)B点关于y轴的对称点坐标为;
(2)将△AOB向左平移3个单位长度,再向上平移2个单位长度得到△A1O1B1 , 请画出△A1O1B1;
(3)在(2)的条件下,△AOB边AB上有一点P的坐标为(a,b),则平移后对应点P1的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题: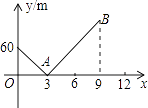
(1)弟弟步行的速度是m/分,点B的坐标是;
(2)线段AB所表示的y与x的函数关系式是;
(3)试在图中补全点B以后的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
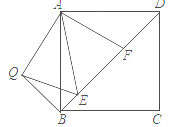
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com