
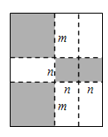
【题目】如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为![]()
![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]()
![]() 的小正方形,五块是长宽分别是
的小正方形,五块是长宽分别是![]()
![]() 、
、![]()
![]() 的全等小矩形,且
的全等小矩形,且![]() .
.
(1)用含![]() 的代数式表示切痕的总长为
的代数式表示切痕的总长为 ![]() ;
;
(2)若每块小矩形的面积为![]() ,四个正方形的面积和为
,四个正方形的面积和为![]() ,试求该矩形大铁皮的周长.
,试求该矩形大铁皮的周长.
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收贵的价目表如下(注:水费按月份结算,![]() 表示立方米)
表示立方米)
价目表 | |
每月用水量 | 价格 |
不超过 |
|
超出 |
|
超出 |
|
![]() 某户居民1月份和2月份的用水量分别为
某户居民1月份和2月份的用水量分别为![]() 和
和![]() ,则应收水费分别是 元和 元
,则应收水费分别是 元和 元
![]() 若该户居民
若该户居民![]() 月份用水量
月份用水量![]() (其中
(其中![]() ),则应收水费多少元? (用含
),则应收水费多少元? (用含![]() 的式子表示,并化简)
的式子表示,并化简)
![]() 若该户居民
若该户居民![]() 两个月共用水
两个月共用水 ![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 两个月共交水费多少元? (用含
两个月共交水费多少元? (用含 ![]() 的式子表示,并化简)
的式子表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50度.
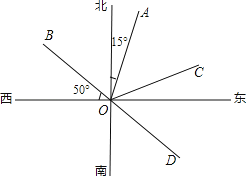
(1)若∠AOC=∠AOB,则OC的方向是 ;
(2)OD是OB的反向延长线,OD的方向是 ;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是 ;
(4)在(1)、(2)、(3)的条件下,∠COE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a,b,其中B,C,E在一条直线上,G在线段CD上,三角形AGE的面积为S.
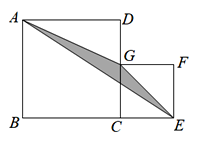
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a,b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上.
①如图1,若∠BCA=90°,∠α=90°,则BE CF;
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 ,使①中的结论仍然成立,并说明理由;
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0
(Ⅰ)当m=![]() 时,求方程的实数根;
时,求方程的实数根;
(Ⅱ)若方程有两个不相等的实数根,求实数m的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式乘方(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)64的展开式中第三项的系数为( )
A. 2016 B. 2017 C. 2018 D. 2019
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com