
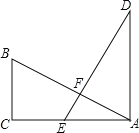
【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.
【答案】(1)AB=DE,AB⊥DE.理由见解析;(2)证明见解析.
【解析】试题分析:(1)根据垂直的定义可证得∠DAE=∠ACB=90°,然后根据ASA可证△ABC≌△DEA,从而得证AB=DE,且∠3=∠1,然后根据直角三角形的内角和等量代换可证得AB⊥DE;
(2)根据三角形的面积和四边形的面积,可知S四边形ADBE= S△ADE+ S△BDE,S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2可得证符合勾股定理的逆定理.
b2可得证符合勾股定理的逆定理.
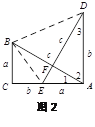
试题解析:(1)解:AB=DE, AB⊥DE.
如图2,∵AD⊥CA,∴∠DAE=∠ACB=90°,
∵AE=BC,∠DAE=∠ACB,AD=AC,∴△ABC≌△DEA,∴AB=DE,
∠3=∠1,∵∠DAE=90°,∴∠1+∠2=90°,∴∠3+∠2=90°,
∴∠AFE=90°,∴AB⊥DE.
(2)如图2,∵S四边形ADBE= S△ADE+ S△BDE=![]() DE·AF+
DE·AF+![]() DE·BF=
DE·BF=![]() DE·AB =
DE·AB =![]() c2,
c2,
S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2,
b2,
∴![]() a2+
a2+![]() b2=
b2=![]() c2,∴a2+b2=c2.
c2,∴a2+b2=c2.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
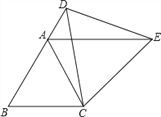
【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边△CDE,连接AE.
(1)求证:△CBD≌△CAE;
(2)求证:AE∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:将连续的偶数2,4,6,8,…,排成如表: 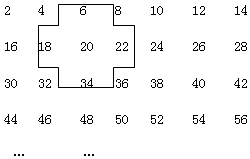
(1)若将十字框上下左右移动,可框住五位数,设中间的数为x,用代数式表示十字框中的五个数的和;
(2)若将十字框上下左右移动,可框住五位数的和能等于2000吗?如能,写出这五位数,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国最长的河流长江全长约为6300千米,用科学记数法表示为( )
A.63×102千米
B.6.3×102千米
C.6.3×103千米
D.6.3×104千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中不能判定两个直角三角形全等的是( )
A. 两条直角边分别对应相等 B. 两个锐角分别对应相等
C. 一条直角边和斜边分别对应相等 D. 一个锐角和一条斜边分别对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下新定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
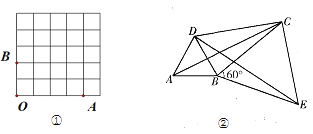
(1)如图①,请你在图中画出格点M,使得四边形OAMB是以OA、OB为勾股边且对角线相等的勾股四边形;
(2)如图②,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,CE.若∠DCB=30°,则四边形ABCD是勾股四边形,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种濒危动物的数量每年以10%的速度减少,n年后该动物数量p与现有数量m之间的关系是p=m(1-10%)n.已知该动物现有数量为8000只,则3年后该动物还有( )
A. 5832 B. 5823 C. 4000 D. 5000
查看答案和解析>>
科目:初中数学 来源: 题型:
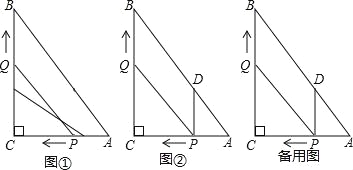
【题目】如图①,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,点P,Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t妙(t≥0).
(1)若三角形CPQ是等腰三角形,求t的值.
(2)如图②,过点P作PD∥BC,交AB于点D,连接PQ;
①是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度.
②当t取何值时,△CPQ的外接圆面积的最小?并且说明此时△CPQ的外接圆与直线AB的位置关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com